Het ECMWF ensemble en (extreme) onzekerheid op de (U)LT.

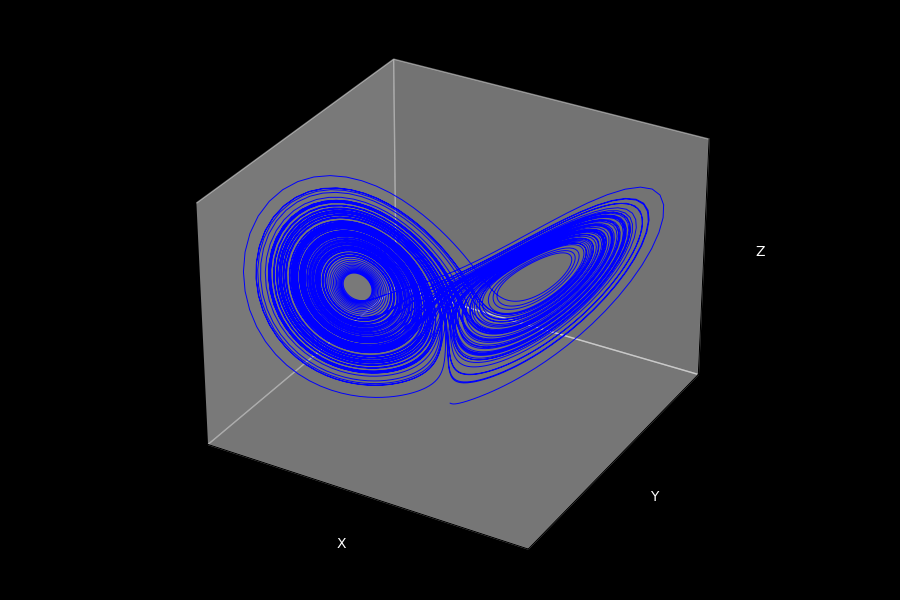
Ensemble Prediction Systems, zoals die van ECMWF, tonen vaak een steeds groter wordend verschil tussen de verschillende ensembleleden op de (U)LT. De oorzaak hiervan is de chaostheorie. De chaostheorie beschrijft dat marginale initiële-waarde-afwijkingen ervoor zorgen dat er in de toekomst grote verschillen optreden. Een NWP-model, zoals ECMWF, heeft inherent te maken met de chaostheorie. Dit komt doordat de atmosfeer een niet-lineair dynamisch systeem is, waarbij deterministische chaos optreedt. De Lorenz-attractor, met de vlinderachtige vorm, wordt geproduceerd door diverse differentiaalvergelijkingen en laat het chaotische patroon goed zien (afbeelding 1) .

De Lyapunov-exponent beschrijft de mate van 'chaos' binnen een dynamisch systeem. Bij een λ van beneden de 0 nemen de verstoringen af, bij een λ van 0 is er geen toename of afname en bij een λ boven de 0 is er sprake van toenemende verstoringen. Bij een λ van >0 is de chaostheorie standaard gezien van toepassing. Ieder NWP-model heeft dus een λ van >0, aangezien er sprake is van de chaostheorie bij atmosferische processen.

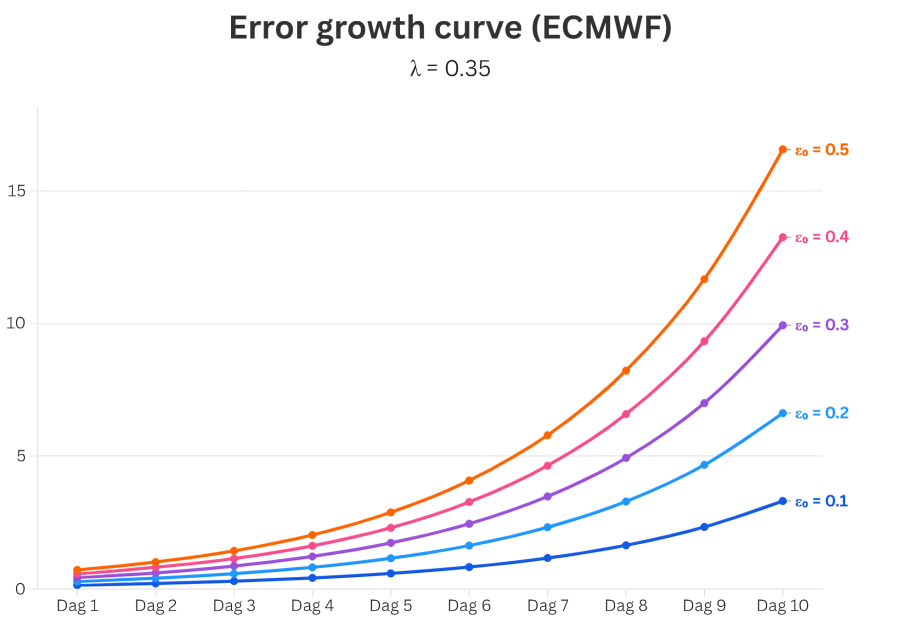
De maximale Lyapunov-exponent van de operationele run van het ECMWF-model wordt beschouwd als 0.35/d, met een range van <0.32;0.41>/d (Bednár et al., 2021). Ik heb een grafiek gemaakt (afbeelding 2) van de growth error curve die verbonden is aan λ = 0.35/d met initial-value afwijkingen van [0.1, 0.5]. De growth error curve toont aan hoe de verwachtingsfout toeneemt over tijd. De growth error curve is een exponentiële lijn, de groeifout neemt dus exponentieel toe. Bij een initiële-waarde-afwijking van 0.1 op dag 1 is de afwijking op dag 10 ongeveer 3.31 en bij een initiële-waarde-afwijking van 0.5 op dag 1 is de afwijking op dag 10 ongeveer 16.56. Aangezien ieder ensemblelid binnen het ECMWF-EPS een andere begintoestand heeft, met andere initiële waarden, ontstaat er op de (U)LT een steeds groter tussen de verschillende ensembleleden - een zogenoemde bifurcatie. 

Met logaritmische vergelijkingen kan er ook een inschatting van de gemiddelde verwachtingshorizon worden gemaakt. Hierbij maak ik wel een benadering op basis van de Lyapunov-exponent van de operationele run, deze is wellicht anders in het ensemble zelf, maar veel verschillen in de Lyapunov-exponent tussen de operationele run en het ensemble verwacht ik niet. Een voorbeeld van een verwachtingshorizon voor de thermische berekeningen van een ensemble: Als de initiële-waarde-afwijking 0.3°C is en er een acceptabele fout is van -3°C of +3°C, dan is de verwachtingshorizon gemiddeld ±6.5 dagen (1/0.35 x ln(3/0.3)). Over het algemeen weten we de initiële-waarde-afwijkingen niet, maar ze liggen vaak wel tussen de 0.1-0.3 in, waardoor de gemiddelde verwachtingshorizon kan worden ingeschat. 

Over het algemeen kan dus worden gesteld dat de onzekerheid binnen een NWP-model exponentieel toeneemt. Dit verklaart waarom er aan het 'einde' van een ensemble vaak een bifurcatie plaatsvindt. In sommige gevallen kan op de ULT het verschil tussen de ensembleleden >20°C zijn, dit past binnen de exponentiële toename van de groeifout. Ook is het een verklaring voor waarom NWP-modellen na een bepaalde tijd (zeer) onbetrouwbaar zijn. In de meteorologie, waaronder op dit forum, wordt er vaak een verwachtingshorizon ingeschat op basis van ervaring. Maar ook op theoretische basis kan er een verwachtingshorizon worden opgesteld, deze geldt voornamelijk voor thermische ontwikkelingen. Bij mesoschale processen is de verwachtingshorizon nog veel kleiner, maar wellicht dat ik binnenkort nog wel een post plaats over mesoschale processen binnen NWP-modellen.