Dank. De strepen ontstaan door lagere bewolking. Dat hangt dan

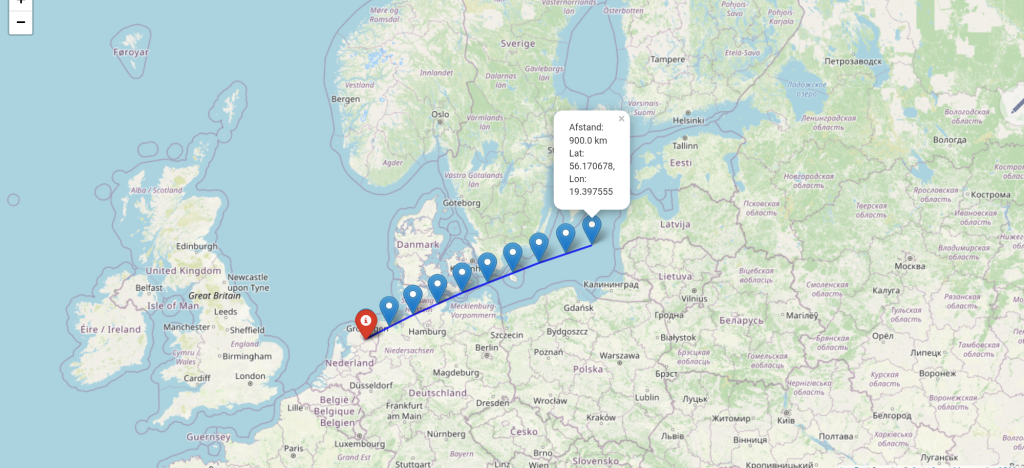
boven de Oostzee ten zuiden van Zweden. Ik heb chatgpt een kaartje laten maken die de lijn van de zon op dat moment volgt en die lijn komt inderdaad boven de Oostzee uit. Dat betekend dus een afstand van zo'n 700 km!

Dit is ook leuk: (bron: Marcel Minnaert, De natuurkunde van 't vrije veld. Deel 1)

https://archief.vakbladeuclides.nl/bestanden/093_2017-18_05_MarcelMinnaert-Natuurkunde_van_t_vrije_veld-Deel_I.pdf

191. Schemeringsstralen.

Als de dagbruid zich baadt, en voor 't schuchter gelaat

Een waaier van vlammen ontplook.

Perk, Iris.

De roosvingerige dageraad.

Homeros.

De schemeringsverschijnselen krijgen een zeer bijzondere schoonheid, als er achter

de westelijke horizon enkele wolken verborgen zitten, wier schaduwstrepen zich

dan als een reuzenwaaier over de avondhemel uitstrekken. Zij stralen uit van het

denkbeeldige punt onder de horizon waar zich de zon bevindt, geheel op de wijze

van het ‘watertrekken’1); maar ditmaal is de hemel zeer helder, en nu zien wij hoe

de donkere bundels zich vooral aftekenen op de plaats van het purperlicht,

waartegenover zij door hun blauwgroene kleur bijzonder goed uitkomen,

te meer, omdat het oog hier nog een subjektief kleurkontrast aan toevoegt. De

schemeringsstralen tonen ons hoe de hemel er zou uitzien als de purperen

verstrooiing ontbrak; nu bemerken we pas hoe ver zich het purperlicht eigenlijk

uitstrekt! Meer dan eens kan men de schemeringsstralen niet alleen aan de zijde

der ondergaande zon waarnemen, maar ook daartegenover aan de oostelijke hemel,

en wel op de purperen achtergrond van de tegenschemering, waar zij in het

tegenpunt van de zon bijeenkomen.

Fig. 150. Schatting van de afstand der wolken, die schemeringsstralen veroorzaken.

Als men schemeringsstralen ziet, verzuime men dus nooit, even naar de Oosthemel

te kijken. Een nauwkeurige waarneming leert, dat de schemeringsstralen aan Oost-

en Westhemel precies twee aan twee met elkaar overeenkomen: het zijn blijkbaar

dezelfde stralen, die eigenlijk over het gehele uitspansel dóórlopen, maar die nabij

de uiteinden het best te zien zijn. Soms is het werkelijk mogelijk, de strepen over

heel hun weg te volgen, als grote bogen die aan hun uiteinden convergeren. We

kennen die lijnen wel, en weten dat het evenwijdige lijnen zijn, die slechts door

gezichtsbedrog gewelfd schijnen (§ 108).

Alleen daar waar verstrooiende deeltjes in de lucht zweven worden de

schemeringsstralen zichtbaar. Bij het ‘watertrekken’ van de zon tekenden zij zich

af in de lichte nevel; bij het purperlicht, in de veel ijlere stofjes die dit

schemeringsverschijnsel veroorzaken. In schemeringen zonder purperlicht ontbreken

ook de schemeringsstralen, en zij vertonen zich nooit tegen de groenige delen van

het uitspansel. Daarentegen kunnen ze nog lang zichtbaar blijven nadat het

purperlicht reeds met de horizontale strepen versmolten is: wel een bewijs dat

eerstgenoemd lichtverschijnsel er nog altijd is, en nog een merkbare bijdrage tot

het licht van de Westerhemel levert.

Dat de schemeringsstralen beter zichtbaar zijn in de buurt van hun

convergentiepunten dan loodrecht daarop, is eigenlijk hetzelfde feit alsdat de

schemeringsverschijnselen sterker zijn in het Oosten en in het Westen dan daar

tussenin. En dit volgt zelf weer uit de verstrooiingswet (vgl. § 183).

We kunnen nog een schatting maken van de afstand waarop de schaduwwerpende

wolk van ons verwijderd is.1) Als die wolk op de aarde rustte, zou de

schemeringsstraal ontstaan op het ogenblik dat de zonnestralen daar aan het

aardoppervlak raken. Wanneer de schemeringsstraal dus zichtbaar is op het ogenblik

dat de zon een hoek α onder de horizon staat, weten we dat de afstand van de wolk

tot ons oog αR bedraagt (R =straal der Aarde). Bevond de wolk zich echter in W op

een hoogte h, dan ziet men uit fig. 150 dat haar afstand tot de waarnemer O alle

waarden hebben kan tussen R(α-&beta en R(α + &beta, naarmate de zon in richtingen

tussen Z1 of Z2

staat, waarbij

of bij benadering

.

Stel dus dat wij een schemeringsstraal waarnemen een half uur na zonsondergang,

dus bij een zonnestand onder de horizon α = 4

o

. De soort wolken die dit verschijnsel

veroorzaken komt stellig niet hoger dan 5 km voor, dus is β op zijn hoogst

= 1/25 rad of 2

o

,3. Bijgevolg komen α - β en α + β overeen met 1,7o

= 0,03 en 6

o

,3

= 0,11; de afstand der wolk ligt dus tussen 190 en 700 km. Zo kan men begrijpen

dat dergelijke schemeringsstralen soms verschijnen, wanneer de lucht voor ons

geheel onbewolkt is.