Het ontstaan van mesocyclonen bij ruimende hoogtewinden
Bericht van: Ben (Lelystad) , 26-08-2006 17:52
Een vraag die mij al langer bezig hield is hoe het kan dat zich in een anticyclonale scheringsomgeving, waar dus de wind ruimt met hoogte, een mesocycloon kan vormen in een buiencel. Uiteindelijk kwam ik uit bij een zeer goed artikel door Bernold Feuerstein in het Duits, wat ik nu even vertaald heb en verder verduidelijkt en aangevuld. Pas wel op, het is absoluut geen makkelijke materie.
Edit: het artikel is nu ook in PDF te downloaden vanaf mijn site (zie link).
Hodogram
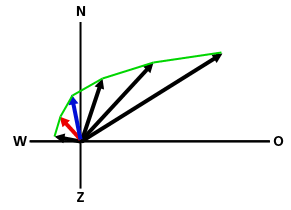De wind kan in de vorm van een vector worden gezien, met de bekende twee componenten van richting en sterkte, waarbij sterkte de windsnelheid voorstelt. Indien we de vectoren van verschillende hoogten in de atmosfeer in een polair diagram (hodogram) tekenen, dan ziet dat eruit zoals in figuur 1.
Te zien is dat de wind op z1 zuidoostelijk en zwak van kracht is, terwijl deze op z6 sterk in snelheid is toegenomen en geruimd is naar zuidwest. Indien we van bovenaf het trajectorie bekijken van een luchtdeeltje dat zich in deze atmosfeer verplaatst, dan zal deze de groene lijn volgen. Het deeltje gaat met de klok mee en maakt dus een anticyclonale beweging. De groene lijn wordt ook wel de hodograaf genoemd.
Vectorveld van horizontaal homogeen windveld
Voor de rest van dit artikel wordt op alle niveaus een horizontaal homogeen windveld verondersteld; dat wil zeggen dat de windvectoren over een geheel gegeven niveau aan elkaar gelijk zijn (homogeen). Visueel ziet dat er uit zoals op figuur 2, waarbij de rode en blauwe pijlen de windvectoren op z2 en z3 voorstellen, net zoals in figuur 1.
Het impulsmoment
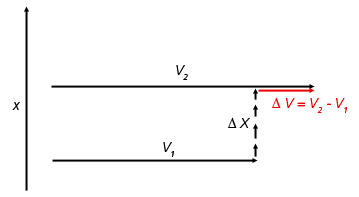Veronderstel allereerst een stroming waarin de snelheidsvector uiteengezet is langs het coordinaat x en loodrecht staat op de stroming. Ter illustratie zijn in figuur 3 twee vectoren v1 en v2 getekend met een willekeurig gekozen afstand ∆x. Voor de rest van het verhaal is enkel het verschil ∆v in vectoren van belang, om preciezer te zijn het snelheidsgradiënt ∆v/∆x.
Voor een toeschouwer die zich met v1 met de stroming meebeweegt, stromen deeltjes (de massa m daarvan is verder niet van belang) met een snelheid ∆v op afstand ∆x voorbij. Deze hebben een impulsmoment van L = m ∆v ∆x , hoewel dit wellicht verbazing zal opwekken omdat het gaat om een lineaire beweging en er niets draait. Dit wordt echter duidelijker als je het voorbeeld van een langsrijdende auto bekijkt, waarbij de toeschouwer zijn hoofd draait om deze te volgen. Zelfs als de afstand tot het object constant verandert, is er ook sprake van een verandering in de hoek.
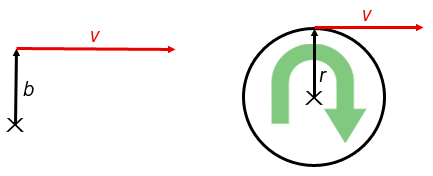
Het impulsmoment van een deeltje, dat op een afstand b met een snelheid v voortbeweegt, is nu gelijk aan dat van een deeltje met gelijke massa dat ronddraait met de snelheid v in een cirkel met radius r = b. Zie figuur 4 voor een illustratieve weergave.
Tot dusver hebben we enkel een windschering in snelheid verondersteld, maar in situaties waarin mesocyclonen voorkomen is ook vrijwel altijd sprake van windschering in de richting. Daarom moeten we gebruik maken van een differentiële manier om het impulsmoment in een dunne, geshearde laag te beschrijven, het zogenaamde rotatievermogen of de vorticiteit van een stromingsveld.
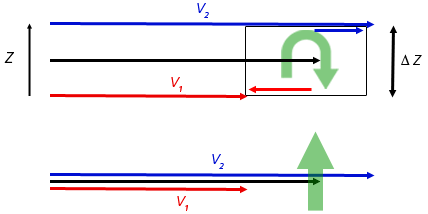
Voor het geval van een mesocycloon wordt een verticale windschering verondersteld, waarbij als we even de pure snelheidsschering nemen de snelheid dus met hoogte toeneemt (in de z-richting), binnen een kleine laag ∆z van v1 naar v2. Het verschil met de gemiddelde windvector (zwart) wordt aangegeven met de kleine rode en blauwe pijltjes, die respectievelijk aan de onderkant naar links wijzen en aan de bovenkant naar rechts. De richting van de rotatie wordt aangegeven door de dikke, groene pijl. Zie figuur 5 op de volgende pagina. De vorticiteit als differentiële verandering in de windvectoren is op zichzelf ook weer een vector, waarvan de kracht wordt bepaald door de verticale snelheidsgradiënten en de richting door de gemiddelde rotatieas.
In het geval van pure snelheidsschering is de vorticiteitsvector horizontaal en staat deze kruisgewijs op de gemiddelde snelheidsvector (de groene pijl in het bovenaanzicht). Dit heet kruisgewijze vorticiteit. Het tegenovergestelde is het geval wanneer er sprake is van pure richtingsschering – hier veranderd enkel de richting, niet de kracht van de vector, met hoogte. Het resultaat is dat de vorticiteitsvector parallel staat aan de gemiddelde snelheidsvector. Dit heet stroomsgewijze vorticiteit.
In de meeste gevallen is er sprake van een combinatie van schering in snelheid en richting. De vorticiteit staat hierbij onder een bepaalde hoek ten opzichte van de gemiddelde snelheidsvector, afhankelijk van de twee scherende componenten. De meridionale component (relatief tot de richting van de gemiddelde windvector) staat in verhouding tot de directionele schering en de transversale component in verhouding tot de snelheidsschering.
Opname van vorticiteit door de stijgstroom
Voor de formatie van mesocyclonen is de meridionale component, parallel aan de stroming, van groot belang. Als door convectie een luchtpakketje geadvecteerd wordt naar de stijgstroom, dan wordt een in eerste instantie horizontale (parallel aan de stroming) rotatieas overgeheld in een verticale rotatieas. In pure snelheidsschering ontbreekt echter de meridionale component en blijft de vorticiteitsvector horizontaal. Zie figuur 6 en 7 op de volgende pagina voor respectievelijk de opnamen van stroomsgewijze en kruisgewijze vorticiteit door een stijgstroom.. Uit de figuren valt gemakkelijk af te leiden waarom een kloksgewijze rotatie van de wind met hoogte uiteindelijk kan leiden tot een cyclonale rotatie in de stijgstroom.
De meridionale component van de vorticiteit die van substationeel belang is voor de rotatie langs de verticale as, is mathematisch uitgedrukt de projectie op de gemiddelde windvector door het nemen van het inwendig product van beide vectoren. Dit is de zogenaamde heliciteit. In de praktijk wordt echter meestal niet gekeken naar de pure heliciteit maar naar de heliciteit relatief ten opzichte van de cel. Daarbij wordt dus rekening gehouden met de onafhankelijke beweging van de cel.
Bronnen
- Wie kommt der Wirbel in den Sturm?, B. Feuerstein
- Sounding-derived parameters associated with severe convective storms in the Netherlands, P. Groenemeijer
- Foto supercell: ©Harald Edens, www.weather-photography.com
Edit: het artikel is nu ook in PDF te downloaden vanaf mijn site (zie link).
Hodogram
De wind kan in de vorm van een vector worden gezien, met de bekende twee componenten van richting en sterkte, waarbij sterkte de windsnelheid voorstelt. Indien we de vectoren van verschillende hoogten in de atmosfeer in een polair diagram (hodogram) tekenen, dan ziet dat eruit zoals in figuur 1.Te zien is dat de wind op z1 zuidoostelijk en zwak van kracht is, terwijl deze op z6 sterk in snelheid is toegenomen en geruimd is naar zuidwest. Indien we van bovenaf het trajectorie bekijken van een luchtdeeltje dat zich in deze atmosfeer verplaatst, dan zal deze de groene lijn volgen. Het deeltje gaat met de klok mee en maakt dus een anticyclonale beweging. De groene lijn wordt ook wel de hodograaf genoemd.
Vectorveld van horizontaal homogeen windveld
Voor de rest van dit artikel wordt op alle niveaus een horizontaal homogeen windveld verondersteld; dat wil zeggen dat de windvectoren over een geheel gegeven niveau aan elkaar gelijk zijn (homogeen). Visueel ziet dat er uit zoals op figuur 2, waarbij de rode en blauwe pijlen de windvectoren op z2 en z3 voorstellen, net zoals in figuur 1.Het impulsmoment
Veronderstel allereerst een stroming waarin de snelheidsvector uiteengezet is langs het coordinaat x en loodrecht staat op de stroming. Ter illustratie zijn in figuur 3 twee vectoren v1 en v2 getekend met een willekeurig gekozen afstand ∆x. Voor de rest van het verhaal is enkel het verschil ∆v in vectoren van belang, om preciezer te zijn het snelheidsgradiënt ∆v/∆x.Voor een toeschouwer die zich met v1 met de stroming meebeweegt, stromen deeltjes (de massa m daarvan is verder niet van belang) met een snelheid ∆v op afstand ∆x voorbij. Deze hebben een impulsmoment van L = m ∆v ∆x , hoewel dit wellicht verbazing zal opwekken omdat het gaat om een lineaire beweging en er niets draait. Dit wordt echter duidelijker als je het voorbeeld van een langsrijdende auto bekijkt, waarbij de toeschouwer zijn hoofd draait om deze te volgen. Zelfs als de afstand tot het object constant verandert, is er ook sprake van een verandering in de hoek.
Het impulsmoment van een deeltje, dat op een afstand b met een snelheid v voortbeweegt, is nu gelijk aan dat van een deeltje met gelijke massa dat ronddraait met de snelheid v in een cirkel met radius r = b. Zie figuur 4 voor een illustratieve weergave.
Tot dusver hebben we enkel een windschering in snelheid verondersteld, maar in situaties waarin mesocyclonen voorkomen is ook vrijwel altijd sprake van windschering in de richting. Daarom moeten we gebruik maken van een differentiële manier om het impulsmoment in een dunne, geshearde laag te beschrijven, het zogenaamde rotatievermogen of de vorticiteit van een stromingsveld.Voor het geval van een mesocycloon wordt een verticale windschering verondersteld, waarbij als we even de pure snelheidsschering nemen de snelheid dus met hoogte toeneemt (in de z-richting), binnen een kleine laag ∆z van v1 naar v2. Het verschil met de gemiddelde windvector (zwart) wordt aangegeven met de kleine rode en blauwe pijltjes, die respectievelijk aan de onderkant naar links wijzen en aan de bovenkant naar rechts. De richting van de rotatie wordt aangegeven door de dikke, groene pijl. Zie figuur 5 op de volgende pagina. De vorticiteit als differentiële verandering in de windvectoren is op zichzelf ook weer een vector, waarvan de kracht wordt bepaald door de verticale snelheidsgradiënten en de richting door de gemiddelde rotatieas.
In het geval van pure snelheidsschering is de vorticiteitsvector horizontaal en staat deze kruisgewijs op de gemiddelde snelheidsvector (de groene pijl in het bovenaanzicht). Dit heet kruisgewijze vorticiteit. Het tegenovergestelde is het geval wanneer er sprake is van pure richtingsschering – hier veranderd enkel de richting, niet de kracht van de vector, met hoogte. Het resultaat is dat de vorticiteitsvector parallel staat aan de gemiddelde snelheidsvector. Dit heet stroomsgewijze vorticiteit.In de meeste gevallen is er sprake van een combinatie van schering in snelheid en richting. De vorticiteit staat hierbij onder een bepaalde hoek ten opzichte van de gemiddelde snelheidsvector, afhankelijk van de twee scherende componenten. De meridionale component (relatief tot de richting van de gemiddelde windvector) staat in verhouding tot de directionele schering en de transversale component in verhouding tot de snelheidsschering.
Opname van vorticiteit door de stijgstroom
Voor de formatie van mesocyclonen is de meridionale component, parallel aan de stroming, van groot belang. Als door convectie een luchtpakketje geadvecteerd wordt naar de stijgstroom, dan wordt een in eerste instantie horizontale (parallel aan de stroming) rotatieas overgeheld in een verticale rotatieas. In pure snelheidsschering ontbreekt echter de meridionale component en blijft de vorticiteitsvector horizontaal. Zie figuur 6 en 7 op de volgende pagina voor respectievelijk de opnamen van stroomsgewijze en kruisgewijze vorticiteit door een stijgstroom.. Uit de figuren valt gemakkelijk af te leiden waarom een kloksgewijze rotatie van de wind met hoogte uiteindelijk kan leiden tot een cyclonale rotatie in de stijgstroom.
De meridionale component van de vorticiteit die van substationeel belang is voor de rotatie langs de verticale as, is mathematisch uitgedrukt de projectie op de gemiddelde windvector door het nemen van het inwendig product van beide vectoren. Dit is de zogenaamde heliciteit. In de praktijk wordt echter meestal niet gekeken naar de pure heliciteit maar naar de heliciteit relatief ten opzichte van de cel. Daarbij wordt dus rekening gehouden met de onafhankelijke beweging van de cel.
Bronnen
- Wie kommt der Wirbel in den Sturm?, B. Feuerstein
- Sounding-derived parameters associated with severe convective storms in the Netherlands, P. Groenemeijer
- Foto supercell: ©Harald Edens, www.weather-photography.com
Bericht laatst bijgewerkt: 26-08-2006 18:18