Gevorderde meteorologie, geostrofische theorie: deel 1
Bericht van: Ben (Lelystad) , 07-10-2006 21:03
Deze posting is een eerste in een reeks van 2 of 3 waarin ik wil ingaan op de quasi-geostrofische theorie, inclusief de daarbij behorende vergelijkingen voor geopotentiële tendens, vorticiteitsadvectie en verticale bewegingen ( ω ). Dat doe ik zowel op wiskundige wijze als illustratief. Aan het eind van de reeks wil ik met behulp van een aantal voorbeelden uit de praktijk de gepresenteerde theorie aantonen. Ik heb bij het schrijven van deze reeks postings, die voor mij vooral ook een leerproces waren, veel geput uit Holton (Introduction to Dynamic Meteorology) en Kurz (Synoptic diagnosis of frontogenetic and cyclogenetic processes). Verder heb ik van diverse websites nog de nodige detailuitleg en verhelderende teksten gebruikt. De illustraties in deze posting zijn naar Holton (2004). De tekst is vast en zeker niet geheel vrij van fouten, maar aanvullingen en correcties ontvang ik graag. Zodra alle delen klaar zijn, zal ik de reeks ook aanbieden in handig Acrobat PDF formaat om alles overzichtelijk af te drukken.
Quasi-geostrofische theorie
Een essentiële eigenschap van de grootschalige stroming in de atmosfeer is dat deze nagenoeg geostrofisch is. Dit betekent dat de wind en massavelden sterk aan elkaar verbonden zijn en ook nagenoeg in balans. Hoewel in een heleboel situaties de geostrofische benadering van de stroming heel nauwkeurig en dus bruikbaar is, is het de subtiele afwijking van geostrofie die van groot belang is om de atmosferische stroming en bepaalde weerfenomenen goed te begrijpen. De theorie neemt de eerder genoemde subtiele afwijkingen in acht maar komt verder zoveel mogelijk overeen met de geostrofische benadering.
Geostrofische benadering
Uit de scalairen van de bewegingsvergelijkingen kan worden opgemaakt van de drukgradiëntkracht nagenoeg volledig gebalanceerd wordt door de Coriolis kracht. Als een eerste benadering kan je dus de geostrofische balansvergelijking opstellen aan de hand van de horizontale bewegingsvergelijkingen:
De balans kan grafisch als volgt worden weergegeven:
waarbij Fdg de kracht uitgeoefend door de drukgradiëntkracht voorstelt en Fc de kracht uitgeoefend door de Coriolis kracht. Het resultaat is de geostrofische beweging (Vg).
Uit de vergelijking voor geostrofische balans kan worden opgemaakt dat er geen netto kracht wordt uitgeoefend op een luchtdeeltje dat zich geostrofisch voortbeweegt. Dit impliceert dat de beweging parallel is aan de isobaren en met een uniforme snelheid. We kunnen de windsnelheid berekenen aan de hand van de geostrofische balansvergelijking. Dit wordt de geostrofische wind genoemd:
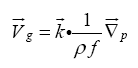
De drukverdeling bepaald dus de geostrofische wind. De geostrofische balansvergelijking is weliswaar een diagnostische vergelijking voor de windsnelheid, maar kan niet worden gebruikt om de evolutie van het windsnelheidsveld te bepalen.
Quasi-geostrofische benadering
Eén van de doelen van dynamische theorie is om de tijdevolutie van velden die van invloed zijn op atmosferische bewegingen te bepalen, met andere woorden om een verwachting te maken van deze velden voor toekomstige tijdstippen. Het mag duidelijk zijn dat de geostrofische benadering geen goede benadering is voor dit doel. De wetten voor het behoud van impuls, massa en energie vormen een danige begrenzing voor verstoringen op synoptische schaal, dat bij benadering het driedimensionale snelheidsveld vrijwel geheel bepaald wordt door het geopotentiële veld. Gebruikmakend van deze benadering is de horizontale snelheid, in de eerste orde, gelijk aan de geostrofische wind. De tijdafgeleiden zijn nagenoeg gelijk:
Op basis hiervan kunnen de quasi-geostrofische vergelijkingen voor thermodynamica en vorticiteit worden afgeleid. Belangrijk om te weten is wel dat de horizontale wind niet wordt vervangen in de term voor divergentie! Dit is omdat de divergentie van de geostrofische wind erg klein is. Het zijn juist de kleine verstoringen in de horizontale wind ten opzichte van de geostrofische balans die voor divergentie zorgen.
In de quasi-geostrofische vergelijking voor vorticiteit kan de divergentieterm worden vervangen door de continuïteitsvergelijking:
Het uiteindelijke resultaat is twee vergelijkingen met twee onbekenden. De geostrofische vorticiteit en de geostrofische wind zijn functies van het geopotentiaal (sigma kan ook worden geschreven als een functie van het geopotentiaal). Vanuit deze vergelijkingen kunnen weer twee andere vergelijkingen worden afgeleid om de evolutie van het geopotentiële veld te bepalen en om het verticale bewegingsveld te bepalen. Deze vergelijkingen zijn respectievelijk de geopotentiële tendensvergelijking en de omega vergelijking.
De geopotentiële tendensvergelijking
Als we de geopotentiële tendens definiëren als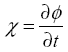
, de thermodynamische vergelijking en vorticiteit vergelijking combineren en tot slot ω elimineren, dan krijgen we de geopotentiële tendensvergelijking:
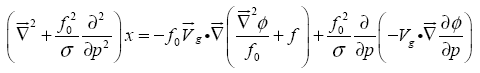
De linkerkant van de vergelijking bevat alleen de ruimtelijke tweede afgeleiden van het tendensveld. Voor golfvormige verstoringen (in alle drie dimensies) is deze term proportioneel aan de negatieve geopotentiële tendens. De factor van proportionaliteit is afhankelijk van de wortels van de golflengten in de drie richtingen.
Differentiële vorticiteitsadvectie
De eerste term aan de rechterkant is proportioneel aan de advectie van absolute vorticiteit. Voor verstoringen in de westelijke stromingen, is de advectie van relatieve vorticiteit en planetaire vorticiteit tegengesteld aan elkaar. De advectie van relatieve vorticiteit heeft de neiging om de verstoring naar het oosten te verplaatsen, terwijl de advectie van planetaire vorticiteit juist de neiging heeft om de verstoring naar het westen te verplaatsen. Voor kortere golven, met een golflengte van minder dan circa 3000 kilometer, domineert de advectie van relatieve vorticiteit, terwijl voor grootschaligere verstoringen juist de planetaire vorticiteit domineert. In onderstaand figuur is een golfvormige verstoring getekend met daarin de verdeling van vorticiteit en vorticiteitsadvectie:
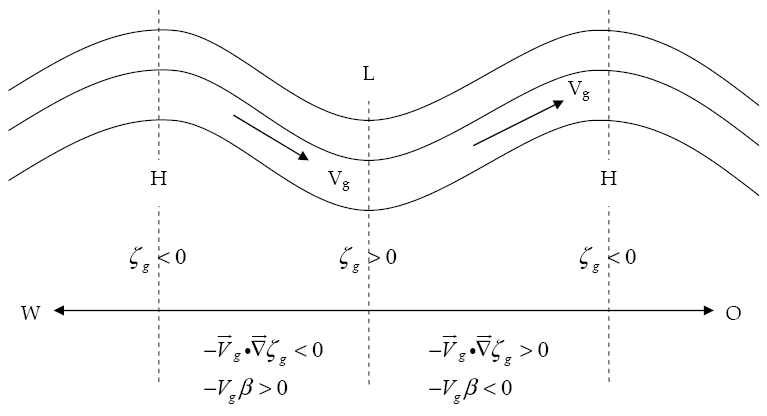
De vorticiteitsadvectie is 0 in de rugassen en trogassen. Dit betekent dat de vorticiteitsadvectie niet de amplitude kan veranderen van de verstoring. Vorticiteitsadvectie werkt daar dus als voortbewegingsmechanisme van de verstoring.
Differentiële dikteadvectie
De tweede term aan de rechterkant van de geopotentiële tendensvergelijking is de differentiële dikteadvectie (of differentiële temperatuuradvectie, aangezien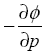
proportioneel is aan de temperatuur). Deze term heeft de neiging om op zijn maximum te zijn in de assen van ruggen en troggen in een ontwikkelende barokliene golf. Het is de differentiële temperatuuradvectie die verantwoordelijk is voor de amplificatie of afbraak van een verstoring. In onderstaand figuur is de faseverandering van de patronen in verhouding tot de hoogte weergegeven.
Hogerop in de atmosfeer is er nauwelijks sprake van een faseverschuiving en liggen de rug- en trogassen nagenoeg op dezelfde plaats. Dit betekent dat het diktepatroon nagenoeg uniform is, met andere woorden er is nauwelijks sprake van een diktegradiënt en dus ook weinig dikteadvectie. Op de lagere niveaus echter is er een sterke faseverschuiving, resulterend in een sterk diktegradiënt en dus ook sterke dikteadvectie.
Bijvoorbeeld onder een rug op 500 hPa is er sterke warmteadvectie bij een warmtefront, terwijl er onder een trog op 500 hPa sprake is van sterke kouadvectie bij een koufront. Het eerste doet de dikte toenemen, zodat de rug in de bovenlucht verder ontwikkelt, terwijl het tweede juist de dikte doet afnemen en de trog in de bovenlucht laat uitdiepen.
Quasi-geostrofische theorie
Een essentiële eigenschap van de grootschalige stroming in de atmosfeer is dat deze nagenoeg geostrofisch is. Dit betekent dat de wind en massavelden sterk aan elkaar verbonden zijn en ook nagenoeg in balans. Hoewel in een heleboel situaties de geostrofische benadering van de stroming heel nauwkeurig en dus bruikbaar is, is het de subtiele afwijking van geostrofie die van groot belang is om de atmosferische stroming en bepaalde weerfenomenen goed te begrijpen. De theorie neemt de eerder genoemde subtiele afwijkingen in acht maar komt verder zoveel mogelijk overeen met de geostrofische benadering.
Geostrofische benadering
Uit de scalairen van de bewegingsvergelijkingen kan worden opgemaakt van de drukgradiëntkracht nagenoeg volledig gebalanceerd wordt door de Coriolis kracht. Als een eerste benadering kan je dus de geostrofische balansvergelijking opstellen aan de hand van de horizontale bewegingsvergelijkingen:
De balans kan grafisch als volgt worden weergegeven:
waarbij Fdg de kracht uitgeoefend door de drukgradiëntkracht voorstelt en Fc de kracht uitgeoefend door de Coriolis kracht. Het resultaat is de geostrofische beweging (Vg).
Uit de vergelijking voor geostrofische balans kan worden opgemaakt dat er geen netto kracht wordt uitgeoefend op een luchtdeeltje dat zich geostrofisch voortbeweegt. Dit impliceert dat de beweging parallel is aan de isobaren en met een uniforme snelheid. We kunnen de windsnelheid berekenen aan de hand van de geostrofische balansvergelijking. Dit wordt de geostrofische wind genoemd:
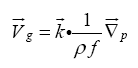
De drukverdeling bepaald dus de geostrofische wind. De geostrofische balansvergelijking is weliswaar een diagnostische vergelijking voor de windsnelheid, maar kan niet worden gebruikt om de evolutie van het windsnelheidsveld te bepalen.
Quasi-geostrofische benadering
Eén van de doelen van dynamische theorie is om de tijdevolutie van velden die van invloed zijn op atmosferische bewegingen te bepalen, met andere woorden om een verwachting te maken van deze velden voor toekomstige tijdstippen. Het mag duidelijk zijn dat de geostrofische benadering geen goede benadering is voor dit doel. De wetten voor het behoud van impuls, massa en energie vormen een danige begrenzing voor verstoringen op synoptische schaal, dat bij benadering het driedimensionale snelheidsveld vrijwel geheel bepaald wordt door het geopotentiële veld. Gebruikmakend van deze benadering is de horizontale snelheid, in de eerste orde, gelijk aan de geostrofische wind. De tijdafgeleiden zijn nagenoeg gelijk:
Op basis hiervan kunnen de quasi-geostrofische vergelijkingen voor thermodynamica en vorticiteit worden afgeleid. Belangrijk om te weten is wel dat de horizontale wind niet wordt vervangen in de term voor divergentie! Dit is omdat de divergentie van de geostrofische wind erg klein is. Het zijn juist de kleine verstoringen in de horizontale wind ten opzichte van de geostrofische balans die voor divergentie zorgen.
In de quasi-geostrofische vergelijking voor vorticiteit kan de divergentieterm worden vervangen door de continuïteitsvergelijking:
Het uiteindelijke resultaat is twee vergelijkingen met twee onbekenden. De geostrofische vorticiteit en de geostrofische wind zijn functies van het geopotentiaal (sigma kan ook worden geschreven als een functie van het geopotentiaal). Vanuit deze vergelijkingen kunnen weer twee andere vergelijkingen worden afgeleid om de evolutie van het geopotentiële veld te bepalen en om het verticale bewegingsveld te bepalen. Deze vergelijkingen zijn respectievelijk de geopotentiële tendensvergelijking en de omega vergelijking.
De geopotentiële tendensvergelijking
Als we de geopotentiële tendens definiëren als
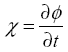, de thermodynamische vergelijking en vorticiteit vergelijking combineren en tot slot ω elimineren, dan krijgen we de geopotentiële tendensvergelijking: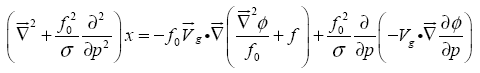 De linkerkant van de vergelijking bevat alleen de ruimtelijke tweede afgeleiden van het tendensveld. Voor golfvormige verstoringen (in alle drie dimensies) is deze term proportioneel aan de negatieve geopotentiële tendens. De factor van proportionaliteit is afhankelijk van de wortels van de golflengten in de drie richtingen.
Differentiële vorticiteitsadvectie
De eerste term aan de rechterkant is proportioneel aan de advectie van absolute vorticiteit. Voor verstoringen in de westelijke stromingen, is de advectie van relatieve vorticiteit en planetaire vorticiteit tegengesteld aan elkaar. De advectie van relatieve vorticiteit heeft de neiging om de verstoring naar het oosten te verplaatsen, terwijl de advectie van planetaire vorticiteit juist de neiging heeft om de verstoring naar het westen te verplaatsen. Voor kortere golven, met een golflengte van minder dan circa 3000 kilometer, domineert de advectie van relatieve vorticiteit, terwijl voor grootschaligere verstoringen juist de planetaire vorticiteit domineert. In onderstaand figuur is een golfvormige verstoring getekend met daarin de verdeling van vorticiteit en vorticiteitsadvectie:
De vorticiteitsadvectie is 0 in de rugassen en trogassen. Dit betekent dat de vorticiteitsadvectie niet de amplitude kan veranderen van de verstoring. Vorticiteitsadvectie werkt daar dus als voortbewegingsmechanisme van de verstoring.
Differentiële dikteadvectie
De tweede term aan de rechterkant van de geopotentiële tendensvergelijking is de differentiële dikteadvectie (of differentiële temperatuuradvectie, aangezien
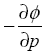proportioneel is aan de temperatuur). Deze term heeft de neiging om op zijn maximum te zijn in de assen van ruggen en troggen in een ontwikkelende barokliene golf. Het is de differentiële temperatuuradvectie die verantwoordelijk is voor de amplificatie of afbraak van een verstoring. In onderstaand figuur is de faseverandering van de patronen in verhouding tot de hoogte weergegeven. Hogerop in de atmosfeer is er nauwelijks sprake van een faseverschuiving en liggen de rug- en trogassen nagenoeg op dezelfde plaats. Dit betekent dat het diktepatroon nagenoeg uniform is, met andere woorden er is nauwelijks sprake van een diktegradiënt en dus ook weinig dikteadvectie. Op de lagere niveaus echter is er een sterke faseverschuiving, resulterend in een sterk diktegradiënt en dus ook sterke dikteadvectie.
Bijvoorbeeld onder een rug op 500 hPa is er sterke warmteadvectie bij een warmtefront, terwijl er onder een trog op 500 hPa sprake is van sterke kouadvectie bij een koufront. Het eerste doet de dikte toenemen, zodat de rug in de bovenlucht verder ontwikkelt, terwijl het tweede juist de dikte doet afnemen en de trog in de bovenlucht laat uitdiepen.