Die vraag houdt velen al enige tijd bezig, met de snelheid waarin de aarde opwarmt en het versnelde tempo waarin dit in west Europa gebeurt, is het slechts een kwestie van tijd voordat ook in Nederland een eerste veertiger zal worden opgetekend. Maar wat is reeël gezien de klimaatprognoses?
Om dat te onderzoeken heb ik gebruik gemaakt van een dataset met hoogste maxima in Nederland over 1901-2006 (dank aan KNMI) en modelgegevens van het ESSENCE project. De gehanteerde prognose van het verloop van de zomertemperatuur voor 1950-2100 is feitelijk een ensemblegemiddelde van 17 modelruns uit het ESSENCE project, allemaal uitgaande van het emissiescenario A1B (zie hier). De prognoses behorende bij dit scenario vertonen vooralsnog de meeste overeenkomst met de realiteit.
Allereerst heb ik over de periode 1901-2006 de herhalingstijd bepaald voor het hoogst behaalde maximum in die periode, namelijk 38,6°C te Warnsveld in 1944. Deze herhalingstijd is bepaald met een uitbreiding op het statistisch pakket R[1], door de datareeks statistisch te fitten (via maximum waarschijnlijkheidsmethodiek) naar een GEV-distributie (GEV = Generalized Extreme Value). Deze distributie leent zich goed voor temperatuurextremen[2], [3], de fit was in het geval van deze reeks beter dan ook wel frequent gebruikte GPD-fit. Met behulp van deze fit is de herhalingstijd voor het grootste extreem vastgesteld op ~100 jaar, met een 95% waarschijnlijkheidsmaximum voor die herhalingstijd van 40,1°C.
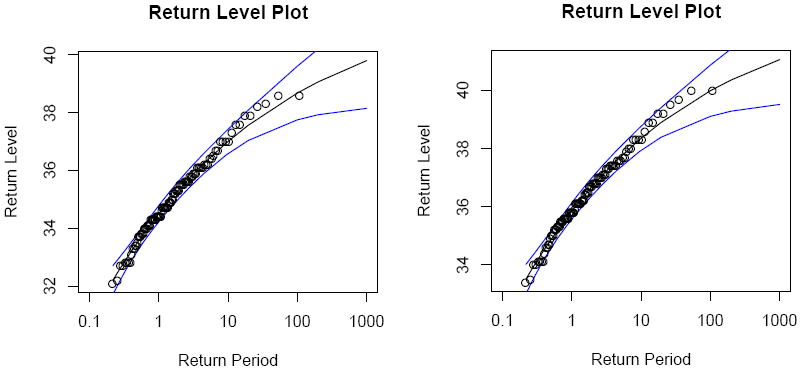
Figuur 1: links de herhalingstijden bij ongewijzigd klimaat, rechts bij 0,9 graad opwarming
Vervolgens heb ik via meervoudige regressie een klein modelletje gemaakt voor het verwachten van de maximale temperatuur in de zomer op basis van de gemiddelde zomertemperatuur, dit model is verder gekalibreerd voor de hoogste waarden. De herhalingstijden van het model en de ruwe gegevensreeks voor de top-10 hoogste waarden komen goed overeen. Vervolgens is met dit model de ruwe reeks getransformeerd conform een bepaalde hoeveelheid opwarming, er is gekozen voor een interval van 0,1°C tot 2,0°C. De temperaturen behorende bij een herhalingstijd van 100 jaar en het 95%-waarschijnlijkheidsmaximum staan hieronder afgebeeld voor een aantal opwarmingssterkten:
Het blijkt dat bij een opwarming van circa 0,9°C t.a.v. het gemiddelde van 1901-2006, de temperatuur behorende bij een herhalingstijd van 100 jaar 40,0 graden bedraagt. Als we nu aannemen dat het 'maximale' dat een temperatuurmaximum in de zomer kan bedragen, in de praktijk doorgaans niet veel meer zal zijn dan de temperatuur behorende bij een herhalingstijd van 100 jaar, dan zou ons klimaat nog 0,9 graad moeten opwarmen om veertigers mogelijk te maken.
Nu is de slotvraag uiteraard: hoe dichtbij zijn we bij circa 0,9 graad opwarming t.a.v. 1901-2006? Om dat te bepalen heb ik een gecombineerde grafiek gemaakt van de waarnemingen van De Bilt en de eerdergenoemde prognose van het ESSENCE project. Weergegeven is een 30-jarig voortschrijdend gemiddelde.
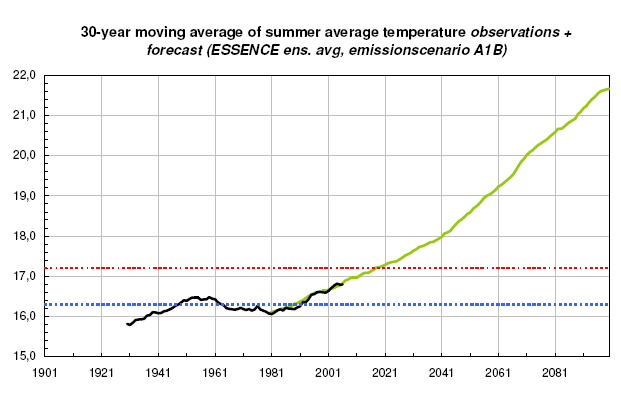
De blauwe stippellijn stelt het gemiddelde over 1901-2006 voor, de rode stippellijn is de grens van 0,9 graad opwarming. Zwart zijn waarnemingen en groen is de modelprognose. Op basis van de prognoses van ESSENCE zullen we tegen 2020 zover zijn dat veertigers een reeële mogelijkheid worden, gegeven dat er dan een zomerseizoen optreedt met vergelijkbare afwijking van de trend als 1944. Opgemerkt moet worden dat dat jaar een véél grotere afwijking had van het gecentreerde 30-jaarsgemiddelde rond dat jaar dan bijvoorbeeld 2003 of 2006 (geëxtrapoleerd via jaargemiddelde). Verder valt uiteraard op dat de modelprognoses over 1950-2006 vooralsnog uitstekend zijn uitgekomen.
Op- en aanmerkingen op deze benadering zijn van harte welkom, wellicht dat er storende fouten inzitten want dit was ook een soort leerprojectje
. Ik heb daarbij dankbaar gebruikt gemaakt van de nodige achtergrondinformatie[4] om de gangbare methodieken te begrijpen.
Gr. Ben
Bronnen:
[1] The Extremes Toolkit: Weather and Climate Applications of Extreme Value Statistics
[2] Kyselý J., 2002: Probability estimates of extreme temperature events: stochastic modelling approach vs. extreme value distributions. Studia geoph. et geod., 46, 93-112
[3] M. Rusticucci, B. Tencer: Changes in extreme temperatures return periods in Argentina
[4] D.Wolters, ,,A method to investigate the time evolution of the probability distribution of high temperature
extremes in The Netherlands, applied to the extremes in the period of May 2006-April 2007''
Om dat te onderzoeken heb ik gebruik gemaakt van een dataset met hoogste maxima in Nederland over 1901-2006 (dank aan KNMI) en modelgegevens van het ESSENCE project. De gehanteerde prognose van het verloop van de zomertemperatuur voor 1950-2100 is feitelijk een ensemblegemiddelde van 17 modelruns uit het ESSENCE project, allemaal uitgaande van het emissiescenario A1B (zie hier). De prognoses behorende bij dit scenario vertonen vooralsnog de meeste overeenkomst met de realiteit.
Allereerst heb ik over de periode 1901-2006 de herhalingstijd bepaald voor het hoogst behaalde maximum in die periode, namelijk 38,6°C te Warnsveld in 1944. Deze herhalingstijd is bepaald met een uitbreiding op het statistisch pakket R[1], door de datareeks statistisch te fitten (via maximum waarschijnlijkheidsmethodiek) naar een GEV-distributie (GEV = Generalized Extreme Value). Deze distributie leent zich goed voor temperatuurextremen[2], [3], de fit was in het geval van deze reeks beter dan ook wel frequent gebruikte GPD-fit. Met behulp van deze fit is de herhalingstijd voor het grootste extreem vastgesteld op ~100 jaar, met een 95% waarschijnlijkheidsmaximum voor die herhalingstijd van 40,1°C.
Figuur 1: links de herhalingstijden bij ongewijzigd klimaat, rechts bij 0,9 graad opwarming
Vervolgens heb ik via meervoudige regressie een klein modelletje gemaakt voor het verwachten van de maximale temperatuur in de zomer op basis van de gemiddelde zomertemperatuur, dit model is verder gekalibreerd voor de hoogste waarden. De herhalingstijden van het model en de ruwe gegevensreeks voor de top-10 hoogste waarden komen goed overeen. Vervolgens is met dit model de ruwe reeks getransformeerd conform een bepaalde hoeveelheid opwarming, er is gekozen voor een interval van 0,1°C tot 2,0°C. De temperaturen behorende bij een herhalingstijd van 100 jaar en het 95%-waarschijnlijkheidsmaximum staan hieronder afgebeeld voor een aantal opwarmingssterkten:
Opwarming Therhaling100 Therhaling100_95%max
0,4 39,3 40,7
0,8 39,9 41,2
0,9 40,0 41,3
Het blijkt dat bij een opwarming van circa 0,9°C t.a.v. het gemiddelde van 1901-2006, de temperatuur behorende bij een herhalingstijd van 100 jaar 40,0 graden bedraagt. Als we nu aannemen dat het 'maximale' dat een temperatuurmaximum in de zomer kan bedragen, in de praktijk doorgaans niet veel meer zal zijn dan de temperatuur behorende bij een herhalingstijd van 100 jaar, dan zou ons klimaat nog 0,9 graad moeten opwarmen om veertigers mogelijk te maken.
Nu is de slotvraag uiteraard: hoe dichtbij zijn we bij circa 0,9 graad opwarming t.a.v. 1901-2006? Om dat te bepalen heb ik een gecombineerde grafiek gemaakt van de waarnemingen van De Bilt en de eerdergenoemde prognose van het ESSENCE project. Weergegeven is een 30-jarig voortschrijdend gemiddelde.
De blauwe stippellijn stelt het gemiddelde over 1901-2006 voor, de rode stippellijn is de grens van 0,9 graad opwarming. Zwart zijn waarnemingen en groen is de modelprognose. Op basis van de prognoses van ESSENCE zullen we tegen 2020 zover zijn dat veertigers een reeële mogelijkheid worden, gegeven dat er dan een zomerseizoen optreedt met vergelijkbare afwijking van de trend als 1944. Opgemerkt moet worden dat dat jaar een véél grotere afwijking had van het gecentreerde 30-jaarsgemiddelde rond dat jaar dan bijvoorbeeld 2003 of 2006 (geëxtrapoleerd via jaargemiddelde). Verder valt uiteraard op dat de modelprognoses over 1950-2006 vooralsnog uitstekend zijn uitgekomen.
Op- en aanmerkingen op deze benadering zijn van harte welkom, wellicht dat er storende fouten inzitten want dit was ook een soort leerprojectje
. Ik heb daarbij dankbaar gebruikt gemaakt van de nodige achtergrondinformatie[4] om de gangbare methodieken te begrijpen.Gr. Ben
Bronnen:
[1] The Extremes Toolkit: Weather and Climate Applications of Extreme Value Statistics
[2] Kyselý J., 2002: Probability estimates of extreme temperature events: stochastic modelling approach vs. extreme value distributions. Studia geoph. et geod., 46, 93-112
[3] M. Rusticucci, B. Tencer: Changes in extreme temperatures return periods in Argentina
[4] D.Wolters, ,,A method to investigate the time evolution of the probability distribution of high temperature
extremes in The Netherlands, applied to the extremes in the period of May 2006-April 2007''