Een luchtdrukverschil van 997-987 hPa = 10 hPa = 1000 Pa over een afstand van 70 km komt neer op een gemiddelde luchtdrukgradiënt van 14 Pa/km. Dat is bijzonder hoog inderdaad. Ik denk dat je bij een gemiddelde storm zo ongeveer uit komt op 5 Pa/km en bij een zeer zware storm op 10 Pa/km.
Dit is mogelijk een gevolg van een sterke verstoring van de hydrostatische balans in combinatie met de wet van behoud van impuls, waarbij laatstgenoemde in het geval van een cirkelvormige beweging tot uiting komt in de zogenaamde centrifugaalkracht. Dit behoeft waarschijnlijk wat verheldering.
Hydrostatische balans
Wanneer er sprake is van een luchtdrukverschil tussen twee punten, dan is er een kracht die we de luchtdrukgradiëntkracht noemen. Deze is gericht van hoge druk richting lage druk en proportioneel met het luchtdrukverschil gedeeld door de afstand.
Naarmate je hoger in de atmosfeer komt neemt de luchtdruk af. Dat betekent dat er dus een opwaartse kracht is. Tegelijkertijd is er de zwaartekracht en dat is juist een neerwaartse kracht. Normaal gesproken zijn deze krachten precies even groot en heffen ze elkaar op. Dit wordt de hydrostatische balans genoemd.
Nu is het zo dat warme lucht een lagere dichtheid heeft dan koude lucht. De benodigde opwaartse luchtdrukgradiëntkracht is daarom ook lager voor warme lucht. Dat heeft tot gevolg dat (in de hydrostatische situatie) de afname van de luchtdruk in een warme luchtmassa langzamer gaat dan in een koude luchtmassa. Plaats je deze luchtmassa's naast elkaar (waarbij ze op 0 meter hoogte dezelfde luchtdruk hebben), dan moet er op enige hoogte sprake zijn van een horizontaal luchtdrukverschil. In de atmosfeer zijn ten minste 4 verschillende situaties te onderscheiden die bovenstaande mooi illustreren.
1. Zeewind
Op een zonnige dag warmt het land sneller op dan de zee, waardoor de luchtlaag in de onderste kilometer zoals hierboven gezegd wat dikker wordt (bijv. 20 meter erbij). Dat zorgt dus voor een horizontaal luchtdrukverschil op enige hoogte waardoor er lucht vanaf de warme zijde richting de koele zijde gaat stromen. Dat wegstromen van de lucht zorgt op hoogte voor een afname van de luchtdruk aan de warme kant en een toename van de luchtdruk aan de koude kant. Aan de warme zijde neemt de verticale luchtdrukgradiënt daardoor toe waardoor de lucht daar omhoog getrokken wordt. Aan de koude zijde neemt de verticale luchtdrukgradiënt af waardoor de lucht naar beneden geduwd wordt. Dat zorgt er weer voor dat de luchtdruk aan de grond toeneemt aan de koude kant en afneemt aan de warme kant. Dit horizontale luchtdrukverschil aan de grond maakt dat de koele zeelucht het land op stroomt.
Dit gaat door totdat de warme lucht boven en de koele lucht onder ligt. Vergelijk het bijv. met water en olie in een fles. Uiteindelijk zie je dat de olie altijd bovenop het water komt te liggen. Ook bij de koude daalstroom uit een onweersbui zie je dat dit gebeurt: de koude lucht kruipt onder de warme lucht en verspreidt zich zoveel mogelijk in alle richtingen. 's Nachts is er soms sprake van een omgekeerde zeewind. Dan stroomt lucht vanaf land richting de zee.
2. Straalstroom
Tussen koude luchtmassa's rond de polen en warme luchtmassa's rond de evenaar is een groot temperatuurverschil, net als bij de situatie met zeewind. Er is echter wel een groot onderscheid: het temperatuurverschil is in dit geval over een afstand van bijv. 1000 km en niet 10 km zoals bij zeewind. Dat zorgt voor een veel kleinere luchtdrukgradiënt en dus een kleine versnelling. De lucht doet er daarom erg lang over om van de warme zijde naar de koude zijde te stromen. Ondertussen wordt de stromende lucht afgebogen door de corioliskracht. Dat afbuigen gaat door totdat de horizontale luchtdrukgradiëntkracht en de corioliskracht elkaar opheffen. Deze evenwichtstoestand wordt de geostrofische balans genoemd. Er stroomt dan geen lucht meer van de warme zijde naar de koele zijde en er vinden dan ook geen stijgende of dalende bewegingen meer plaats (tenzij dit evenwicht verstoord wordt).
3. Convectie
Hier krijgen we de situatie dat een bel met warme lucht (verkregen door de lucht bijv. plotseling te verhitten) rondom geheel omgeven is door koelere lucht. Dankzij de hogere luchtdruk in de warme luchtbel zet deze vrijwel onmiddellijk uit waardoor het luchtdrukverschil opgeheven wordt. Maar tijdens dit uitzetten is de luchtdichtheid afgenomen terwijl de verticale luchtdrukgradiënt hetzelfde is als voor het verhitten. De hydrostatische balans is nu verstoord: de verticale luchtdrukgradiënt is groter dan de zwaartekracht geworden waardoor er netto een opwaartse kracht is. De warme lucht wordt dus naar boven geduwd.
Door de afname van de luchtdruk met de hoogte zal de luchtbel tijdens het stijgen uitzetten. Daar is arbeid voor nodig (de lucht rondom de bel moet weggeduwd worden) en dat gaat ten koste van de inwendige energie: de temperatuur neemt af. Dit gaat met ongeveer 10 graden per kilometer. Tegelijkertijd vindt er (als de luchtvochtigheid 100% is) condensatie plaats: een deel van de waterdamp gaat over in de vloeibare fase. De watermoleculen komen dichter op elkaar te zitten, waardoor een deel van de potentiële energie (die er is ten gevolge van elektrische krachten tussen moleculen) omgezet wordt in warmte: de temperatuur neemt toe. Zolang de luchtbel warmer blijft dan de omgeving zal er een opwaartse kracht zijn.
4. Stingjet
Bij een depressie zal na verloop van tijd maritiem polaire lucht vlak langs de kern met maritiem tropische lucht gaan stromen. Er is dus weer sprake van twee verschillende luchtmassa's die vlak langs elkaar liggen. Op enige hoogte zal de warme lucht richting de koele lucht gaan stromen en vinden er stijgende bewegingen plaats aan de warme zijde en dalende bewegingen aan de koude zijde. Er is echter één probleem: de stijgende lucht in de kern kan niet aangevuld worden met lucht uit de nabije omgeving. Dat komt door impulsbehoud: een deeltje verandert niet van snelheid (grootte en/of richting) tenzij er een netto kracht op werkt. Voor een cirkelvormige beweging komt impulsbehoud openbaar in de centrifugaalkracht die verhindert dat de lucht richting de kern stroomt. Bovenin kan de lucht trouwens wel vrij wegstromen en op bijv. 300 of 500 hPa is dan doorgaans sterke divergentie te zien (te herkennen aan uitwaaierende cirrus op de satellietbeelden).
Vanwege bovenstaand probleem ontstaat er een uitstulping van het lagedrukgebied in de richting van de grootste temperatuurgradiënt. Aan het begin (westelijke richting) van deze uitstulping wordt de luchtstroming versneld (lucht stroomt stukje met de luchtdrukgradiënt mee) en aan het einde (oostelijke richting) weer afgeremd. Tussenin bevindt zich dus een smalle strook met zeer hoge windsnelheden.
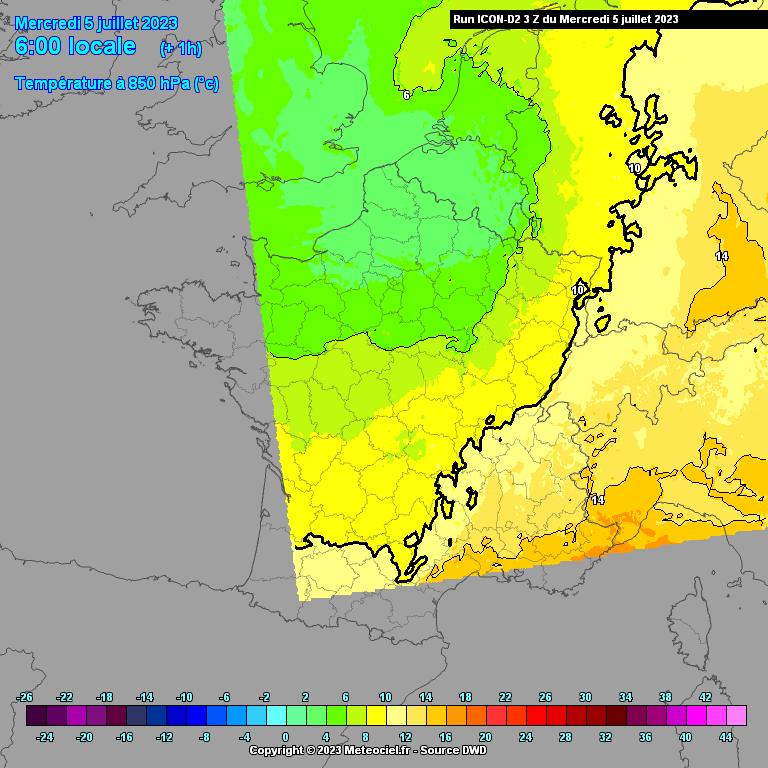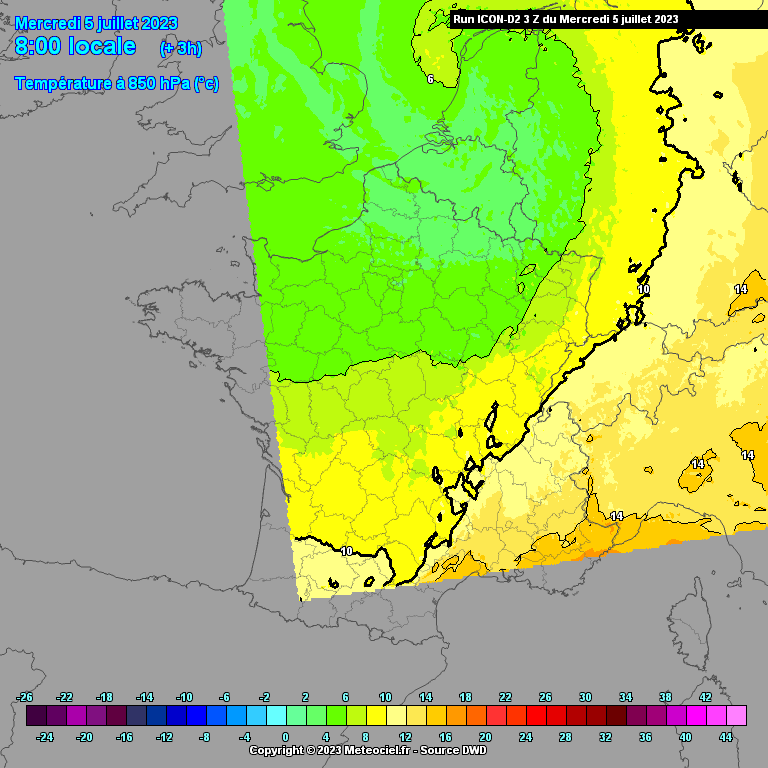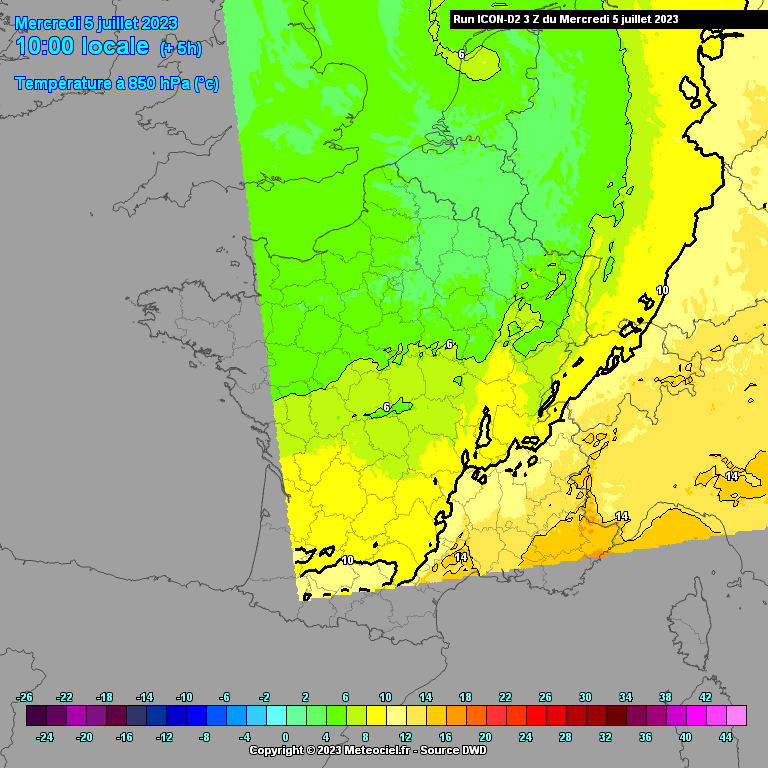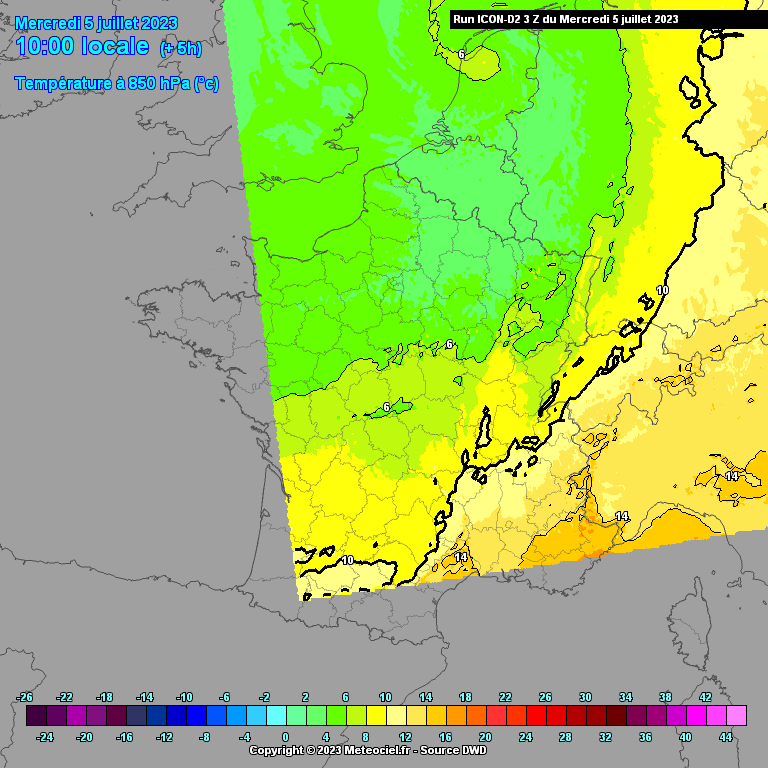
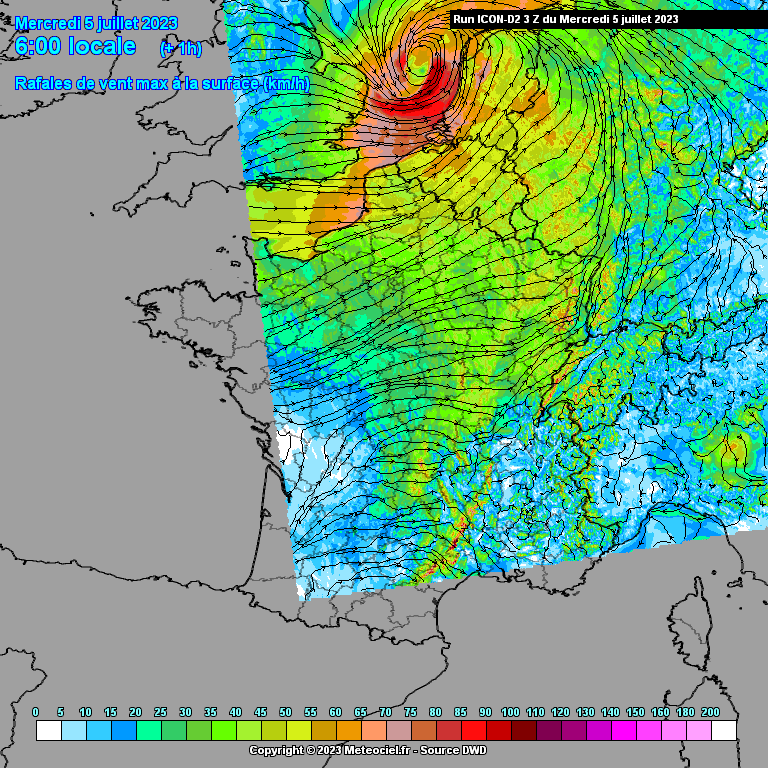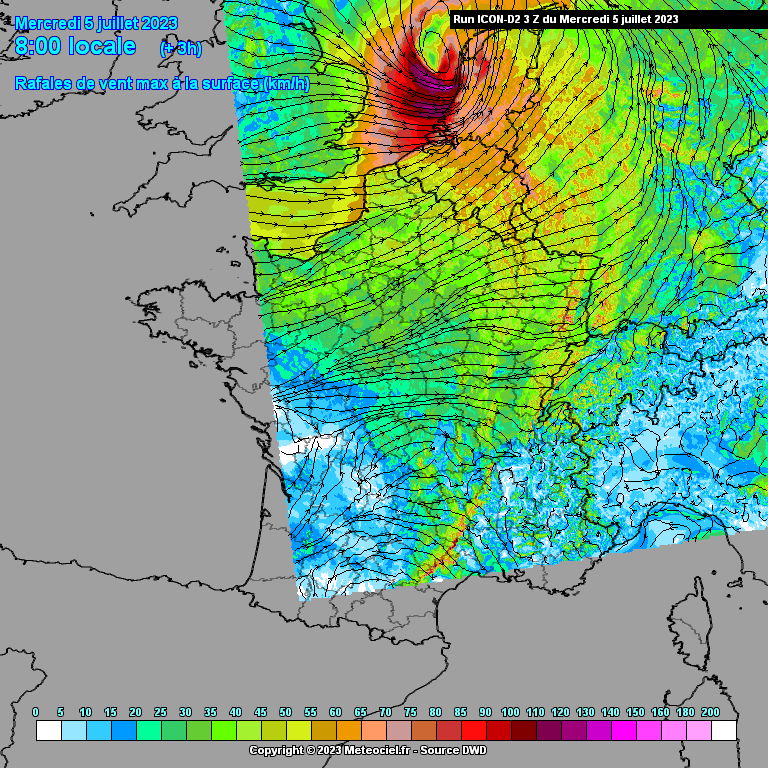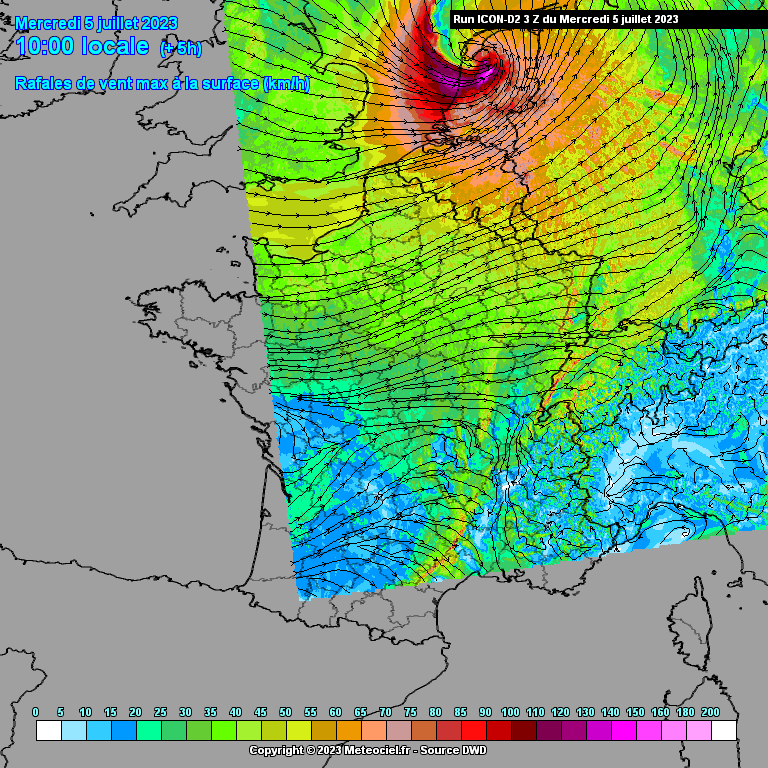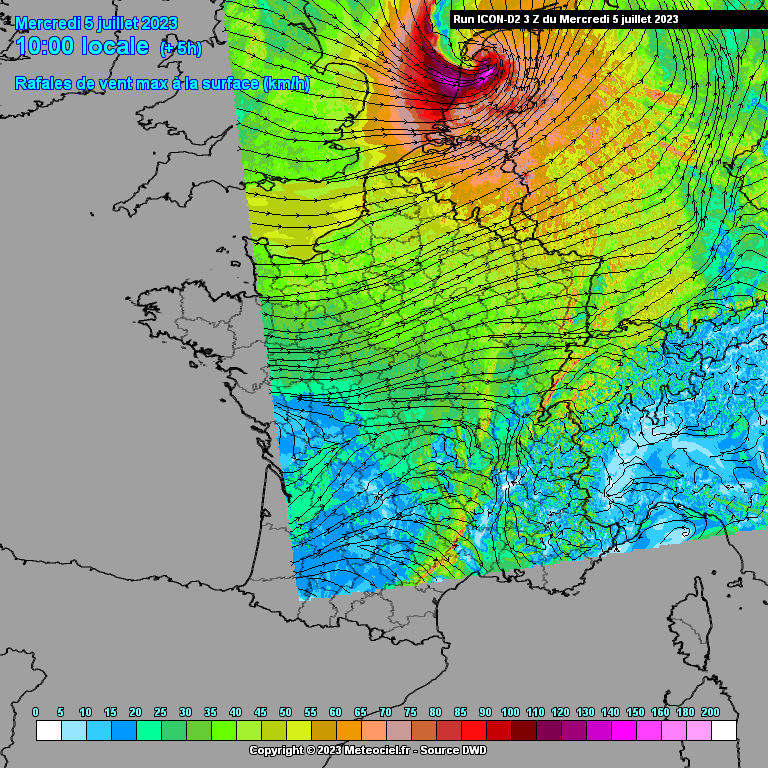
Op onderstaande animatie kun je de uitstulping van lage druk goed zien. Dit was trouwens wel tijdens een eerdere run van ICON-D2 waarbij de windstoten nog niet zo extreem hoog waren. Ik heb deze animatie helaas niet van de laatste run voorafgaand aan de storm (de twee bovenstaande animaties zijn dat wel). Op meteociel is deze run nog wel terug te halen.
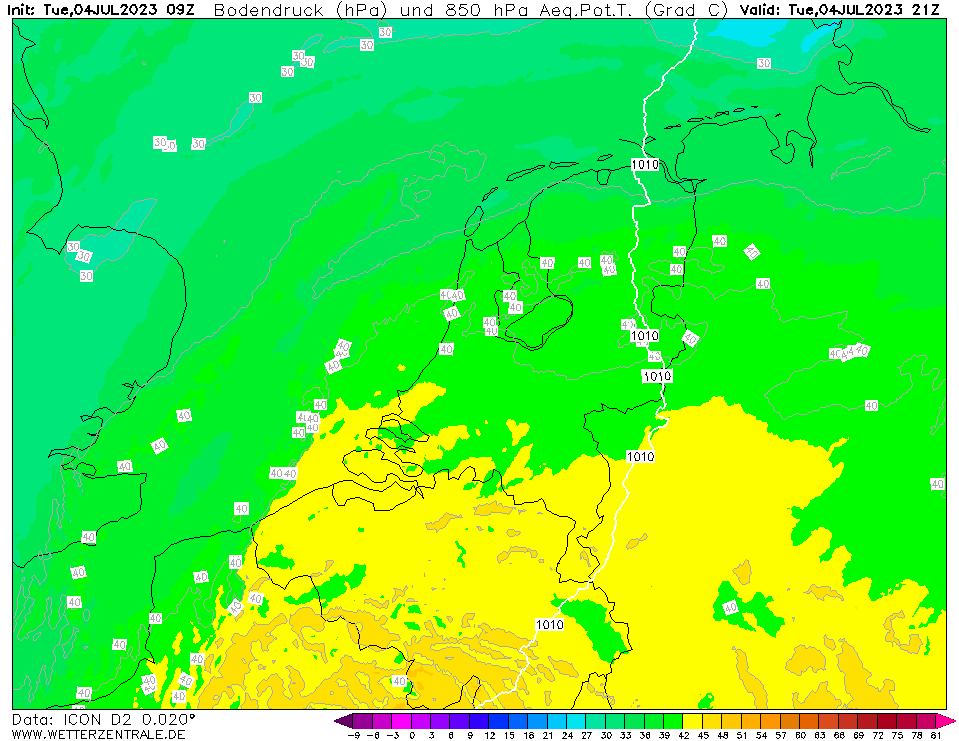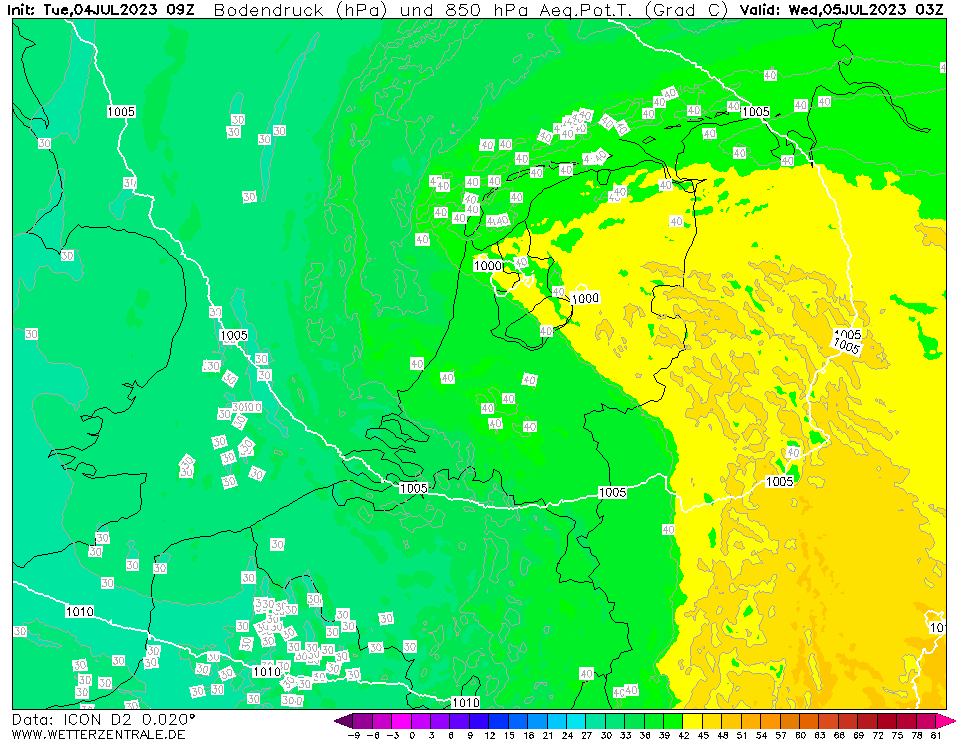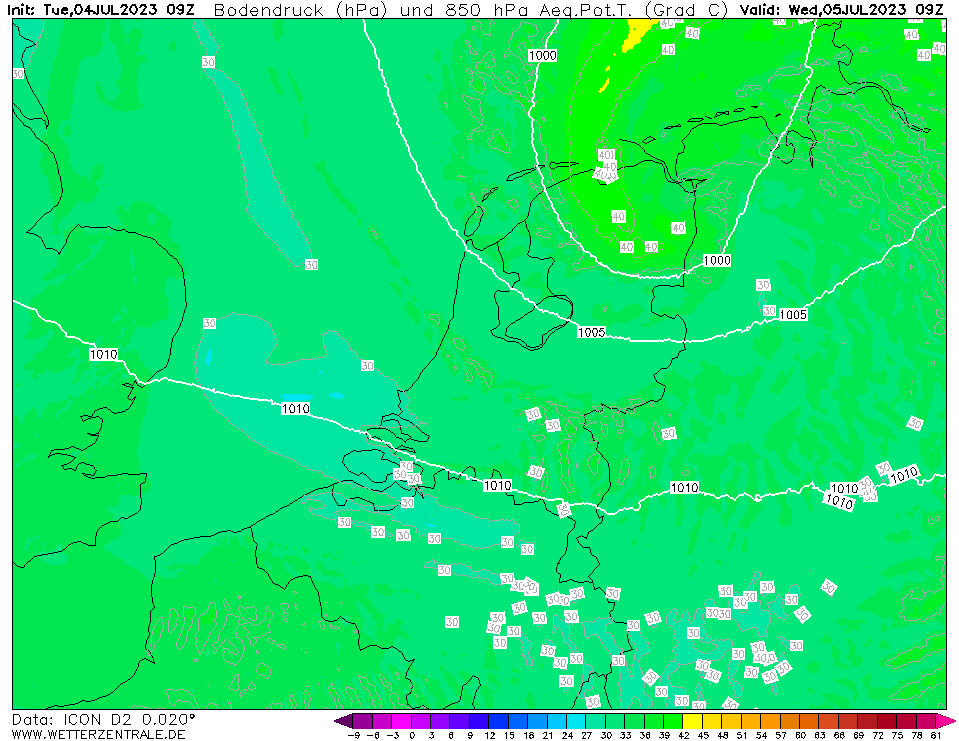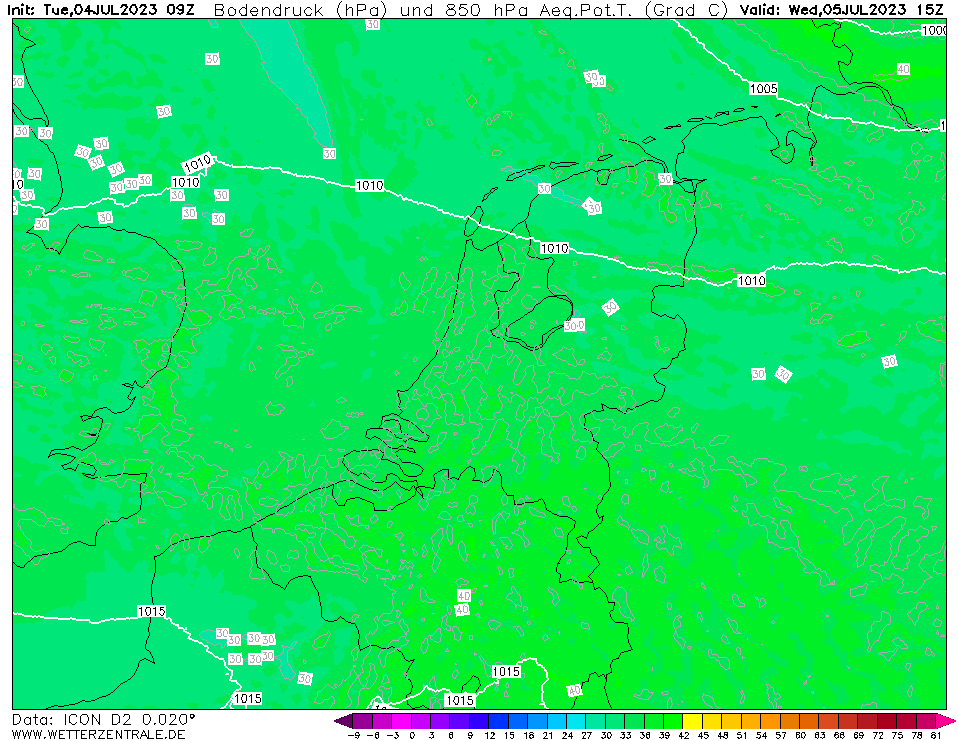
De maximale luchtdrukgradiënt dP/dx kun je uitrekenen door de luchtdrukgradiëntkracht Fgr = m * 1/rho * dP/dx gelijk te stellen aan de centrifugaalkracht Fc = m * v² / r en vervolgens beide kanten te delen door de massa m en te vermenigvuldigen met de luchtdichtheid rho. Dan krijg je dP/dx = rho * v² / r. De luchtdichtheid is ongeveer 1.2 kg/m³, de uurgemiddelde windsnelheid in IJmuiden was 30 m/s en de afstand van IJmuiden tot de kern ongeveer 60 km. Dan kom je op een gradiënt van 1.2 * 30 * 30 / 60 = 18 Pa/km. Dat is hoger dan de 14 Pa/km hierboven, maar dat komt waarschijnlijk doordat 14 Pa/km de gemiddelde waarde van de gradiënt tussen Den Helder en Schiphol is terwijl 18 Pa/km vermoedelijk de maximale waarde van de gradiënt is. Had je een barometer ten noorden en ten zuiden van IJmuiden geplaatst dan zou je vermoedelijk dichtbij die 18 Pa/km uitkomen.
Die hoge waarde komt mede door de kleinschaligheid van de depressie. Bij een kleinere straal moet de gradiëntkracht groter zijn om de lucht af te buigen. Bij een windhoos speelt dit een nog grotere rol: daar is de straal r veel kleiner en de snelheid v hoger waarbij je gemakkelijk op een gradiënt komt die nog eens 1000 maal zo groot is als hier. Wanneer de gradiëntkracht en de centrifugaalkracht precies in evenwicht zijn is er sprake van de cyclostrofische balans.
De maximale windsnelheid zal afhangen van bijv. de temperatuurgradiënt en de beginsnelheid (en die hangt ook weer van heel veel dingen af: sterkte van de straalstroom, eventuele convectie, wrijving boven land/water, scherpte van de hoogtetrog, enzovoort). Deze kan in principe nog veel hoger worden dan de 146 km/h in IJmuiden, maar zulke stormen komen niet vaak voor in West-Europa en dan moet die storm ook nog eens op het hoogtepunt over een onbeschut weerstation aan de kust trekken.
We kunnen een schatting maken van de maximale gemiddelde windsnelheid met behulp van de wet van behoud van energie voor een stroming (Bernoulli): P1 + 0.5 * rho * v1² = P2 + 0.5 * rho * v2². Herschrijven levert op: v2 = sqrt(2*(P1-P2)/rho + v1²
. Laten we P1-P2 = 3 hPa = 300 Pa en v1 = 20 m/s nemen. Dan komen we op v2 = 30 m/s. Deze getallen zijn natuurlijk vooral indicatief en hoeven niet letterlijk genomen te worden. Maar een relatief klein luchtdrukverschil kan al snel voor hoge windsnelheden zorgen.
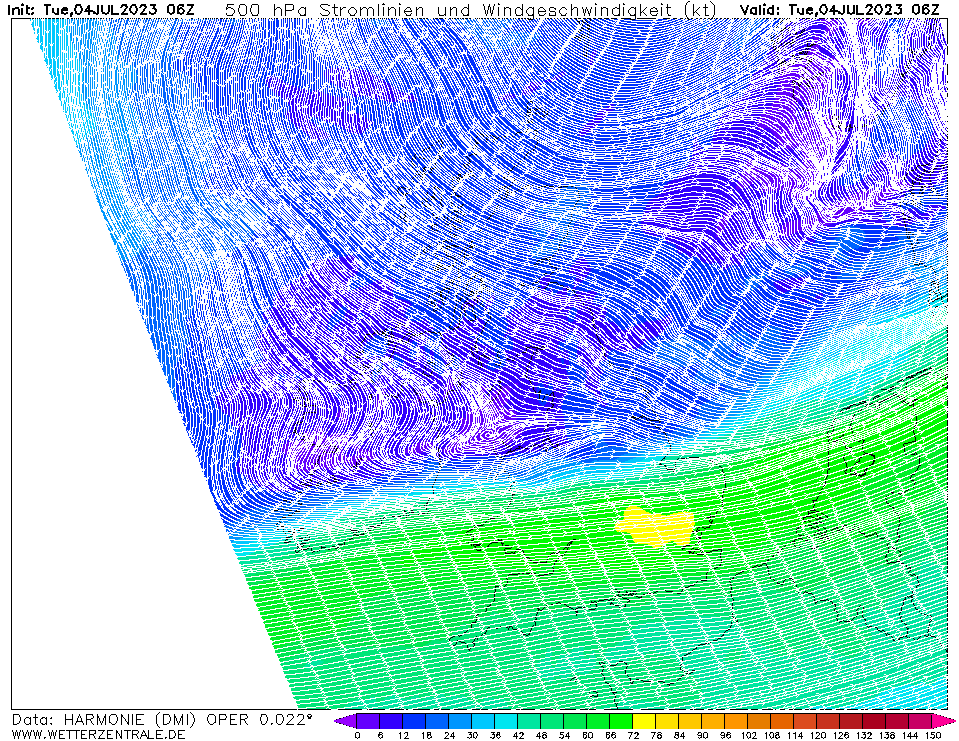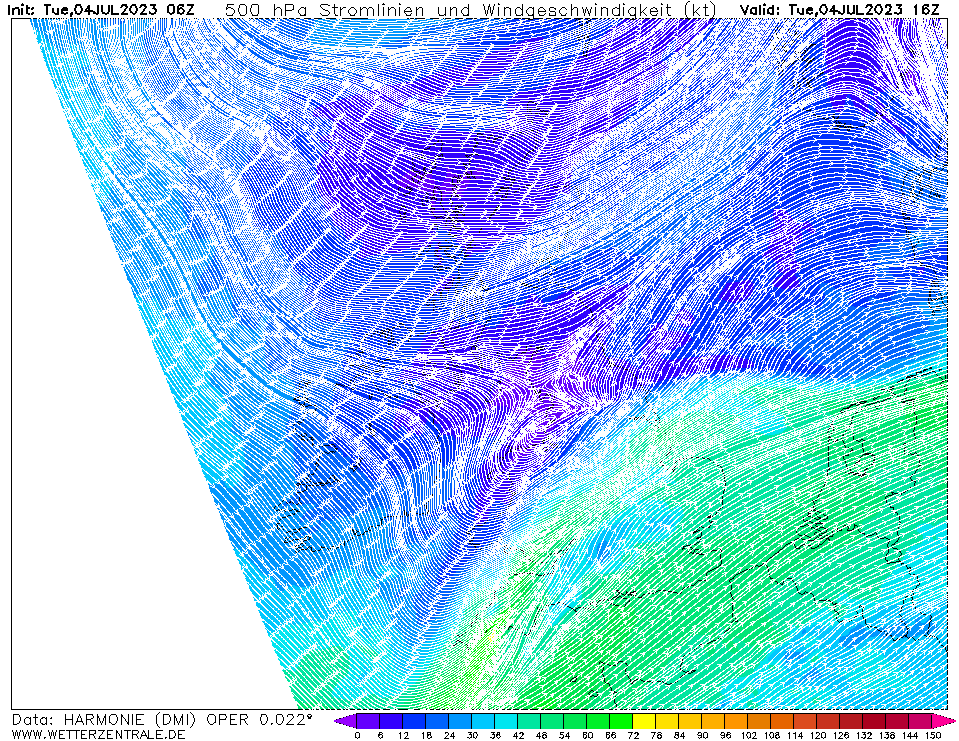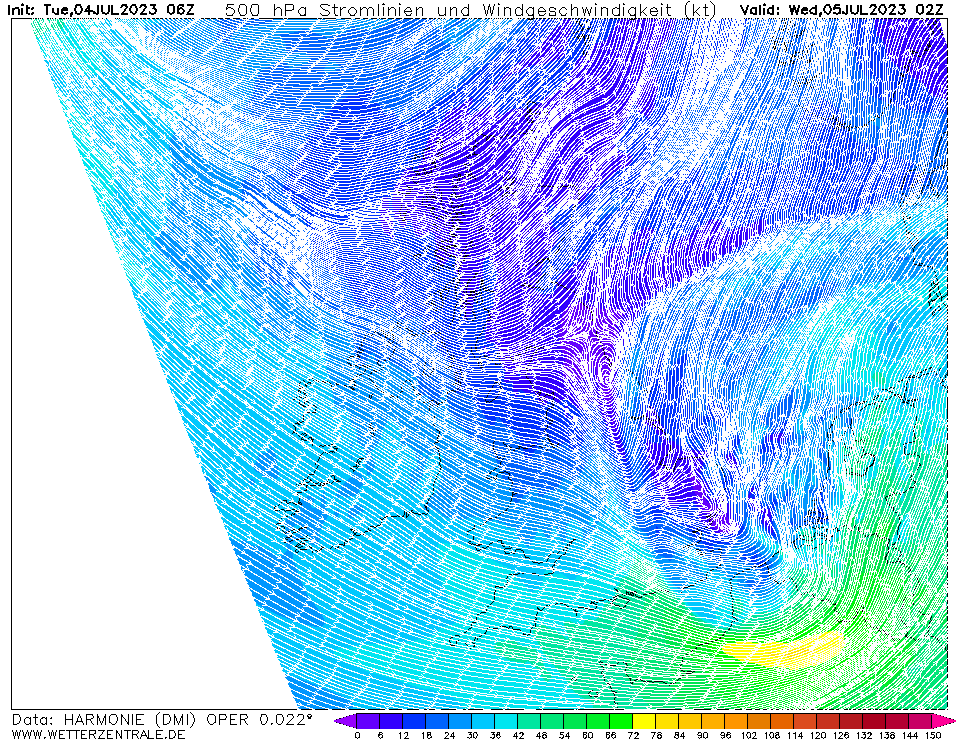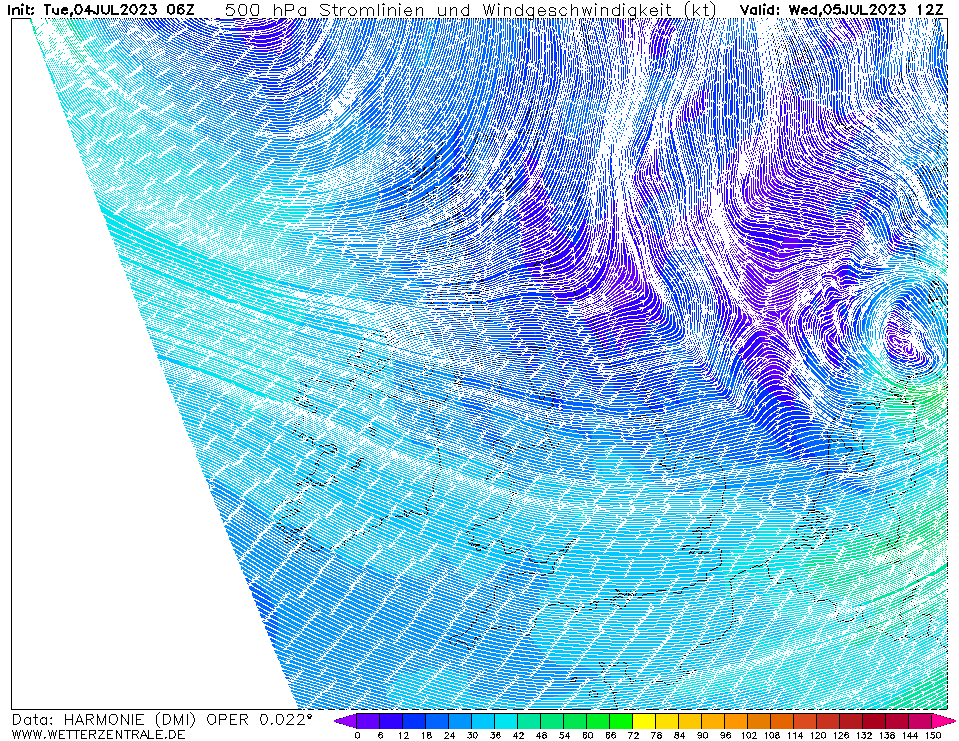
Vaak worden deze hoge windsnelheden aan de straalstroom toegeschreven. Die speelt natuurlijk een rol bij het ontstaan en uitdiepen van een depressie, maar tijdens het optreden van de hoogste windsnelheden was de windsnelheid op 500 hPa zo goed als 0 m/s boven IJmuiden, zie onderstaande animatie. Het kan natuurlijk wel zijn dat de luchtstroom op geringe hoogte (<1 km) aan de grond komt, maar ik heb niet de middelen om dat uit te zoeken.
Bron van bovenstaand verhaal zijn de genoemde natuurwetten. Ik meen dat deze correct toegepast zijn en overeenstemmen met waarnemingen en modellen, maar indien niet dan hoor ik het uiteraard.
