Al jarenlang lijken de problemen bij het KNMI steeds verder toe te nemen en er lijkt geen einde in zicht. In Meteorologica van Maart 2014, ruim tien jaar geleden, vroeg oud-medewerker Henk de Bruin zich al hardop, wellicht enigszins provocerend, af of er niet een hoop kennis verloren is gegaan bij het KNMI (en anderen in de hydrologie/meteorologie). Het KNMI had er verstandig aan gedaan zich dat ter harte te nemen maar koos ervoor om het naast zich neer te leggen.
Vaker wel dan niet communiceert het KNMI niet eerlijk over de methodologie die ze hanteren, exact waar de kritiek van de Bruin over ging. Een van de meest schrijnende voorbeelden is de studie van het KNMI naar de extreme droogte in de Hoorn van Afrika gedurende 2021-2022 (Kimutai et al 2023 & Kimutai et al 2025).
Dit is een artikel daarover op de website van het KNMI zelf:
https://www.knmi.nl/over-het-knmi/nieuws/zonder-klimaatverandering-was-de-huidige-droogte-in-de-hoorn-van-afrika-niet-zo-extreem-geweest-als-nu
In de staatsmedia (nos.nl) doet de medewerker er nog een schepje bovenop:
Onderzoek: kans op droogte in Hoorn van Afrika 100 keer groter door opwarming aarde (https://nos.nl/l/2472996)
Het blog klimaatveranda.nl (van KNMI medewerker Bart Verheggen) gaat helemaal los door het resultaat schokkend te noemen. Ik vind het ook schokkend, maar om hele andere redenen:
https://klimaatveranda.nl/2023/05/05/attributiestudie-klimaatverandering-is-de-hoofdoorzaak-van-de-droogte-in-de-hoorn-van-afrika/
De studie is gedaan volgens de methode die bij het KNMI is ontwikkeld, en het doet pijn het te moeten zeggen maar dit is het inmiddels tragisch nalatenschap van Van Oldenborgh, een soort Trojaanspaard dat alles corrumpeert wat er mee in aanraking komt. Het is echt ongelooflijk hoeveel prominente klimaatwetenschappers en meteorologen dit soort studies direct of indirect gebruiken om "hun punt" te maken.
De grootste fout is wat mij betreft de conceptuele door te denken dat de gebruikte methode voor de berekening van potentiële verdamping geschikt is voor deze toepassing. Dit is beschreven in van Thornthwaite (1948), specifiek Appendix 1. Die methode is het al niet geschikt in algemene zin, het is een van de slechtst beschikbare methoden, dus waarom kiest het KNMI daarvoor? Dat wordt nog erger doordat ze het ver buiten de originele context toepassen, iets waar Thornthwaite zelf ruim 75 jaar geleden voor waarschuwde. De gemaakte aannames zijn niet geldig in aride gebieden zoals de Hoorn van Afrika, en wat mij betreft ook niet in de context van klimaatverandering laat staan tijdens een extreme droogte. Een maandgemiddelde temperatuur is op z'n best een zwakke proxy voor beschikbare energie, in de zin dat als de zon schijnt (in de zomer) er veel netto-energie is en vice versa (voor bv verdamping). In de context van opwarming als gevolg van broeikasgassen (niet de zon!) gaat dat uiteraard niet op. De opwarming is het gevolg van een toename aan inkomende langgolvige straling, en het oppervlak warmt net zo lang op totdat de uitgaande er mee in balans is (enigszins simpel gezegd). Het effect op de netto beschikbare energie is vrij beperkt.
Dit zei Jensen et al (1990) erover in ASCE MOP-70:
".. it has been one of the most misused empirical equations in arid and semi-arid irrigated areas."

Een dergelijke methode vandaag de dag gebruiken, laat staan in de context van klimaatverandering, is echt te gek voor woorden wat mij betreft. En ook totaal onnodig, maar ik vermoed dat de keuze komt omdat de foute implementatie die ze gebruiken een enorm signaal geeft met opwarming (succes gegarandeerd).
Eerst een iets duidelijkere fout welke wellicht wat makkelijker te begrijpen is. In de studie maken ze gebruik van de wereldwijde temperatuurafwijking, het KNMI gebruikt daarvoor NASA GISTEMP. De statistische constructie waarin ze dit toepassen is al vrij bizar. Ze doen een regressie tussen de wereldwijde temperatuurafwijking (x-as) en de lokale neerslag welke log10 geschaald is (y-as). Daarbij wordt de temperatuur bewerkt door een lopend 4 jaar gemiddelde te nemen (zie uitleg op KNMI Climate Explorer). De lokale neerslag is een combinatie van de Centrends & CHIRPS datasets en loopt van 1900-2022. De regressie in de studie ziet er dan alsvolgt uit, hun figuur 5c:
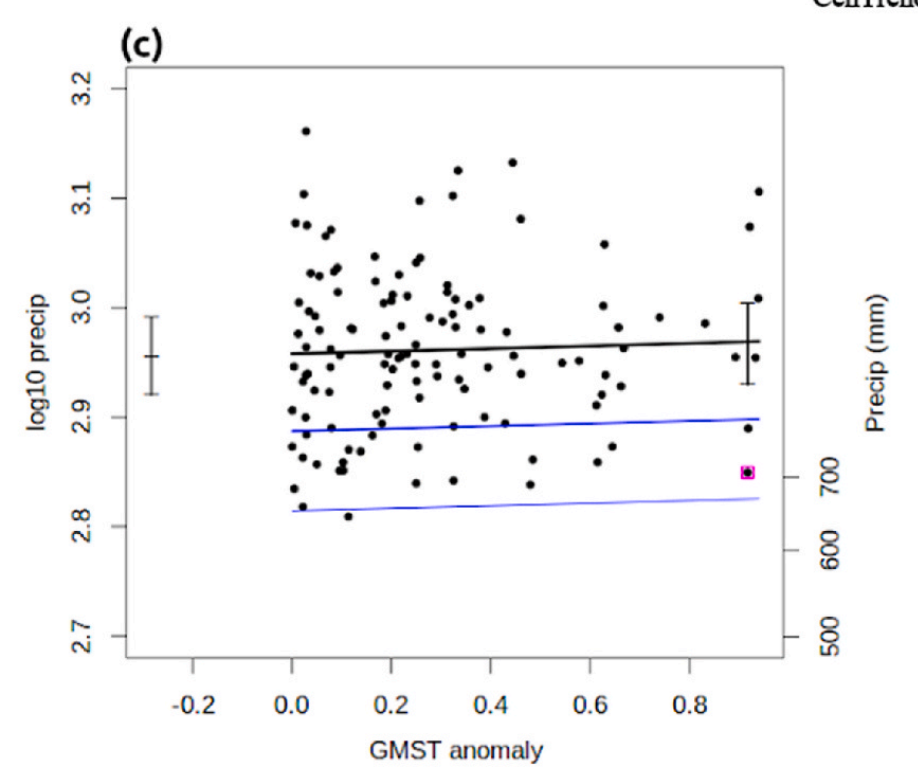
Merk op dat de temperatuur een range heeft van ongeveer 0°C tot iets minder dan 1°C. Dat is opvallend weinig, en omdat in dit geval enkel de relatieve waarde invloed heeft maakt de referentie periode niet zoveel uit (dat is de originele 1951-1980 van GISTEMP in dit geval).
Onderstaande grafiek laat die temperatuur zien, maar ook de originele NASA GISTEMP zien (vergelijkbaar bewerkt met een 4-jaar lopend gemiddelde) en ook nog een andere variant, ook van KNMI Climate Explorer. Het verschil is meteen duidelijk, en op het oog kan je al zien dat dit verschil symmetrisch is rond 0°C. Oftewel, KNMI gebruikt in hun studie de positieve waarde van de temperatuurafwijking ("abs(gmst)" i.p.v. "gmst"). Bizar natuurlijk.
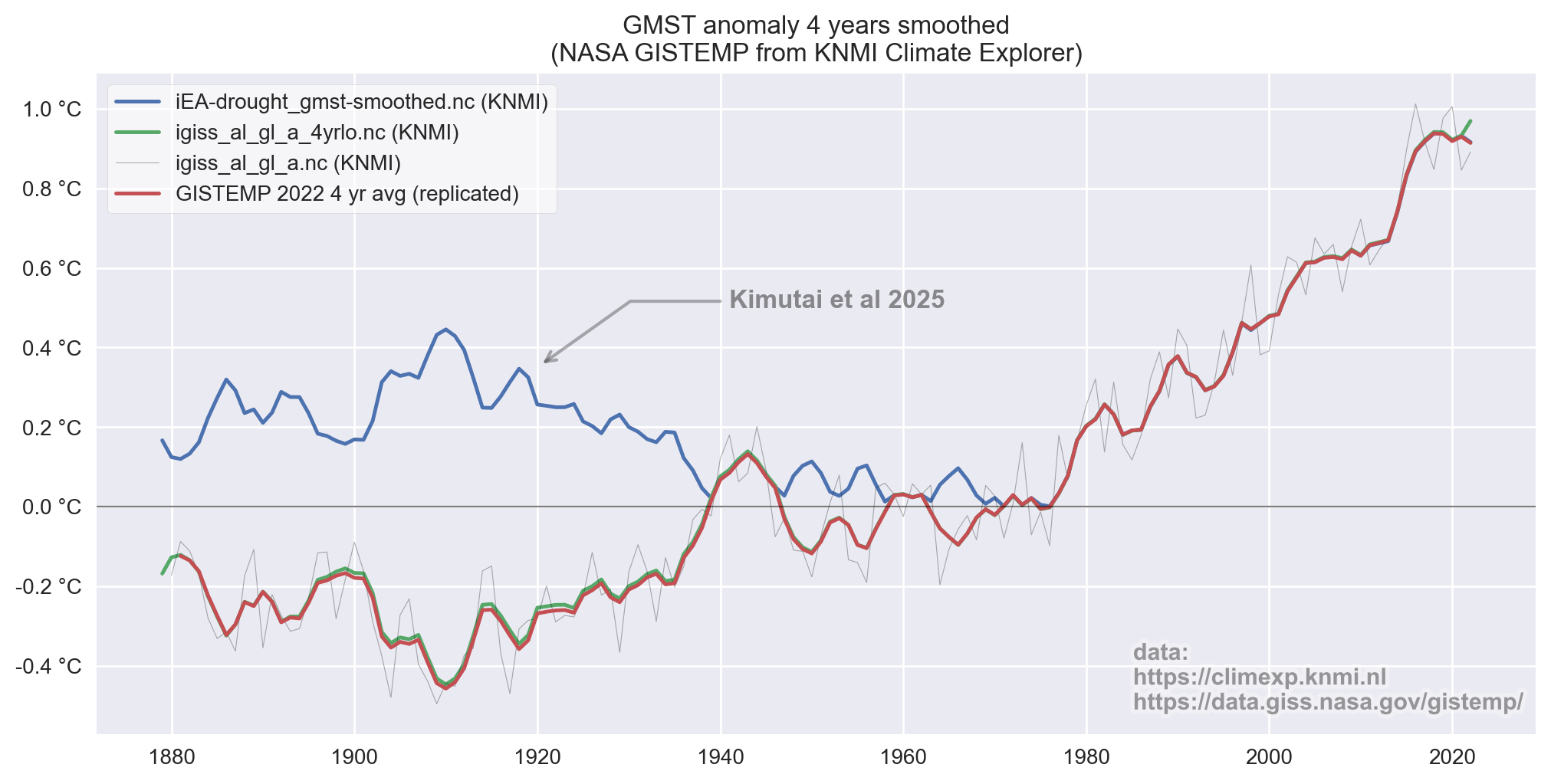
Als ik hun figuur 5c reproduceer, en ook corrigeer ziet het verschil er alsvolgt uit:
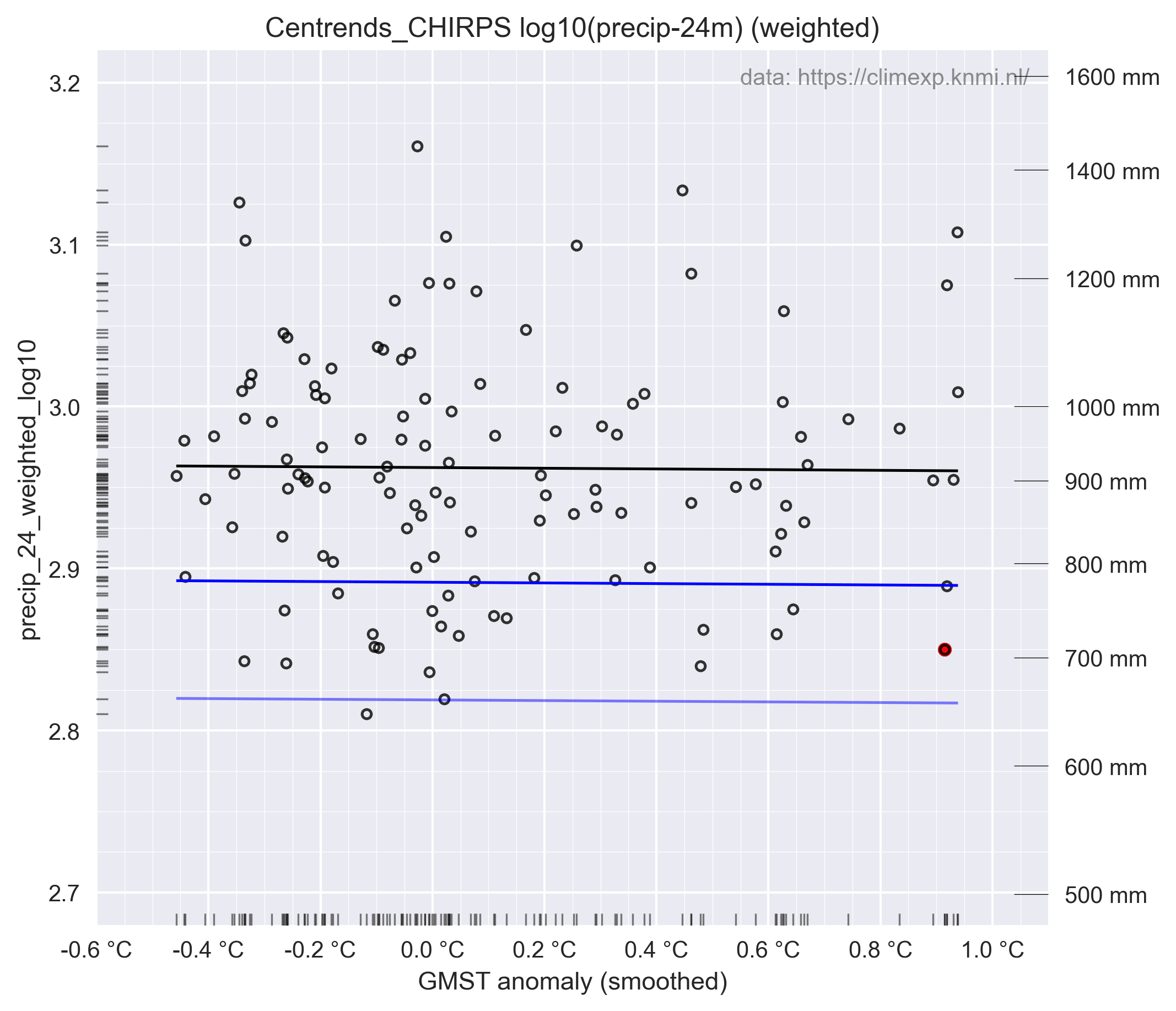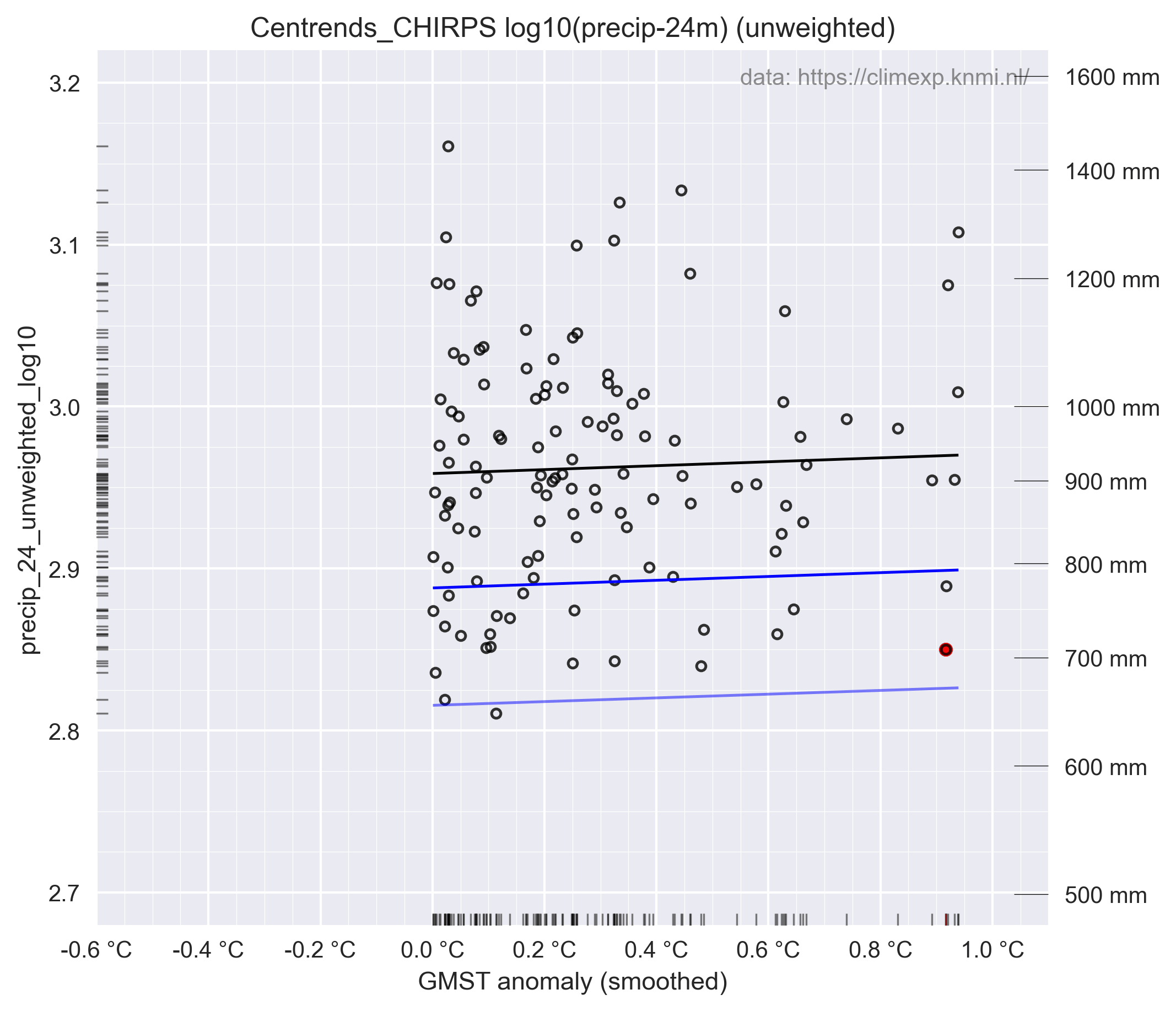
Het blijft een niet-significante trend en hun "probabilty-ratio" verandert dan ook weinig, hun figuur 5d (reproductie & correctie).
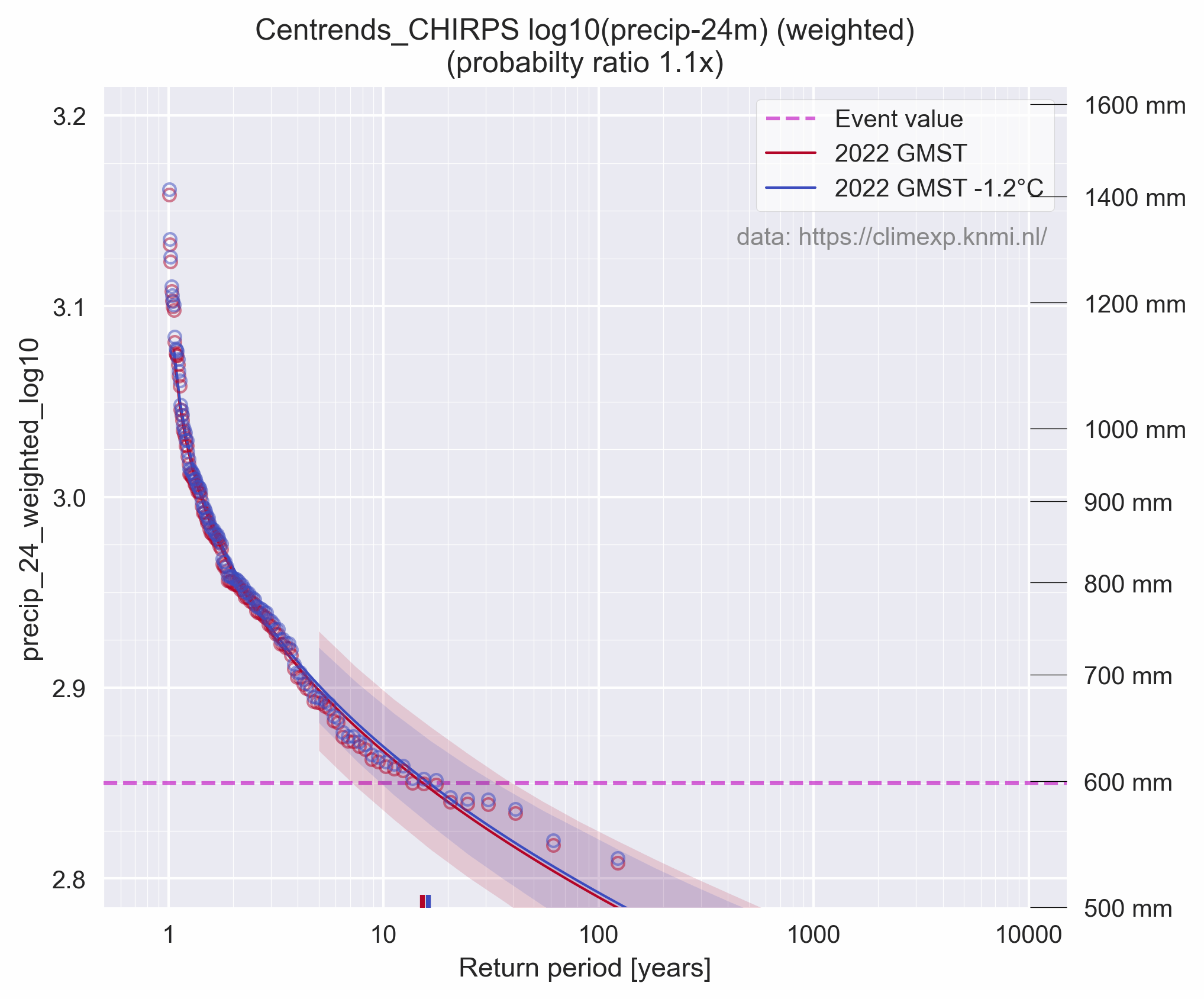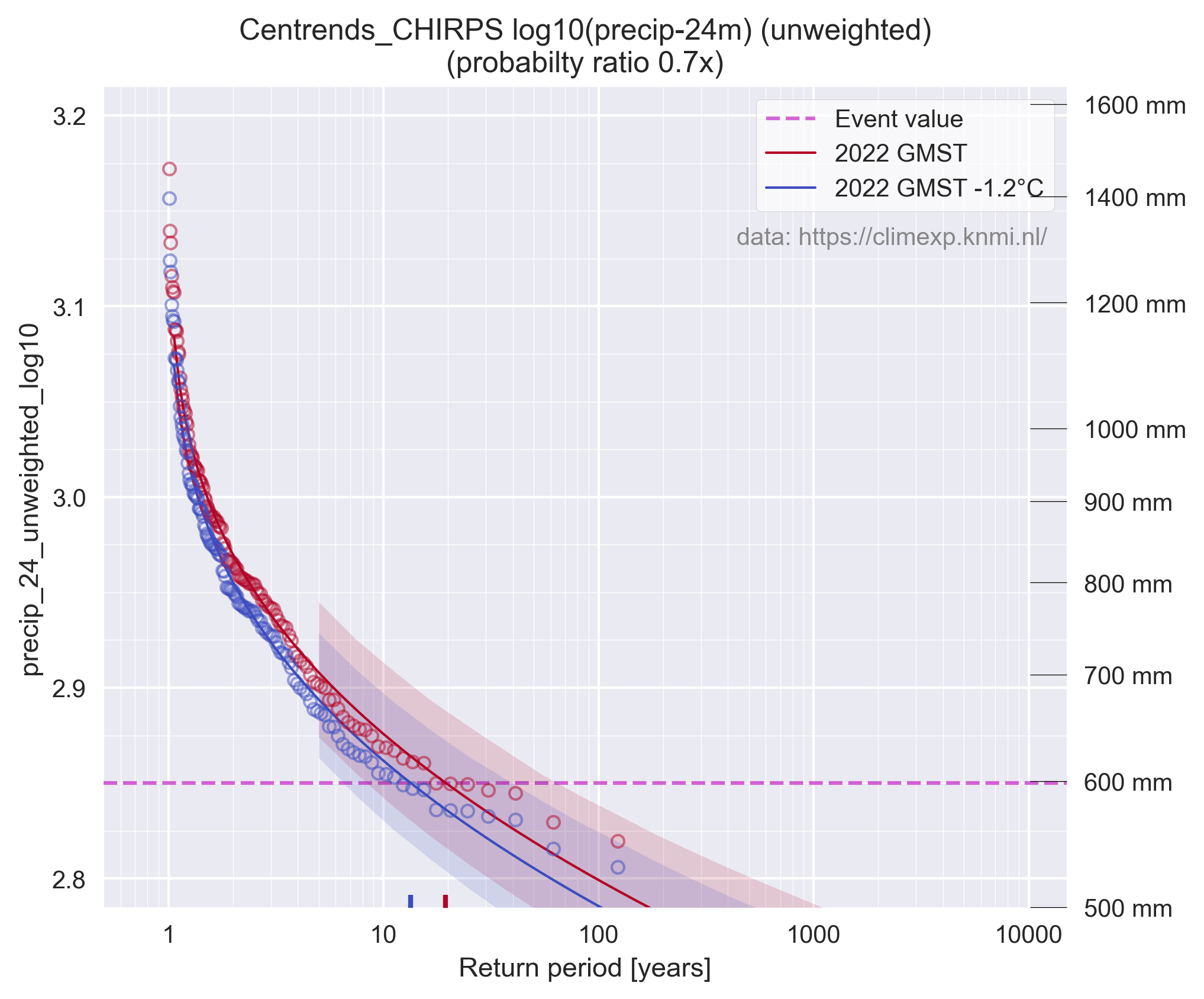
Ze doen ook nog een vergelijkbare handeling maar dan met SPEI-24. Deze berekenen ze door eerst een "neerslagoverschot" te berekenen, het verschil tussen de neerslag en de bovengenoemde potentiële verdamping op basis van Thornthwaite (1948). Omdat daar de temperatuur voor nodig is gebeurt dit slechts vanaf 1980 (op basis van NOAA PSL CPC data). Dat "neerslagoverschot" wordt vervolgens statistisch omgevormd tot de SPEI-24 door een "Generalized Logistic" verdeling te fitten en de daarmee gevonden kans uit te drukken als een Normaalverdeling (Gaussian) met een gemiddelde van 0 en standaarddeviatie van 1. De details van de distributie en manier van fitten (L-moments) zijn te vinden in Hosking & Wallis (1996).
De belangrijkste fout die ze maken in hun implementatie van Thornthwaite (1948) is het weglaten van de correctie voor (maandgemiddelde) temperaturen boven de 26.5°C. De gegeven formules zijn daarboven niet langer geldig en er moet gebruik gemaakt worden van een lookup-table (zie zijn figuur 13). Dit weglaten maakt de methode extreemgevoelig voor temperatuur en resulteert in onrealistisch hoge toename van potentiële verdamping met opwarming. De Hoorn van Afrika (hun aoi) heeft vaak maandgemiddelde temperaturen die daar ruim bovenuit komen. De methode is wat vreemd omdat je 12 maanden (tegelijk) nodig bent om een resultaat voor elk van die maanden te krijgen. Anders gezegd, het temperatuurverloop door het jaar is van invloed op de potentiële verdamping van een enkele maand in dat jaar. Dit maakt het ook wat ongemakkelijk omdat het KNMI ervoor kiest om het op "kalender jaren" toe te passen, hierdoor wordt bijvoorbeeld de potentiële verdamping in maart beïnvloed door de temperatuur later in het jaar (november, december etc). De causaliteit daarvan is natuurlijk nogal dubieus. Logischer zou zijn om het "lopend" toe te passen waarbij voor elke maand de voorgaande 11 maanden gebruikt worden, dat voorkomt tijdreizen.

Een (hypothetisch) voorbeeldje van het effect ziet er voor de tropen uit als op de onderstaande afbeelding. Dit is met een "dubbele sinus" als jaarlijks temperatuurverloop. De onderstaande grafiek geeft de gevoeligheid weer, de verandering in potentiële verdamping bij een toename van de temperatuur. De foute implementatie heeft een snel toenemende gevoeligheid terwijl de correcte implementatie boven de 26.5°C juist een afnemende gevoeligheid heeft. Dit maakt natuurlijk gigantisch veel uit in de context van opwarming, het hele uitgangspunt van deze studie.
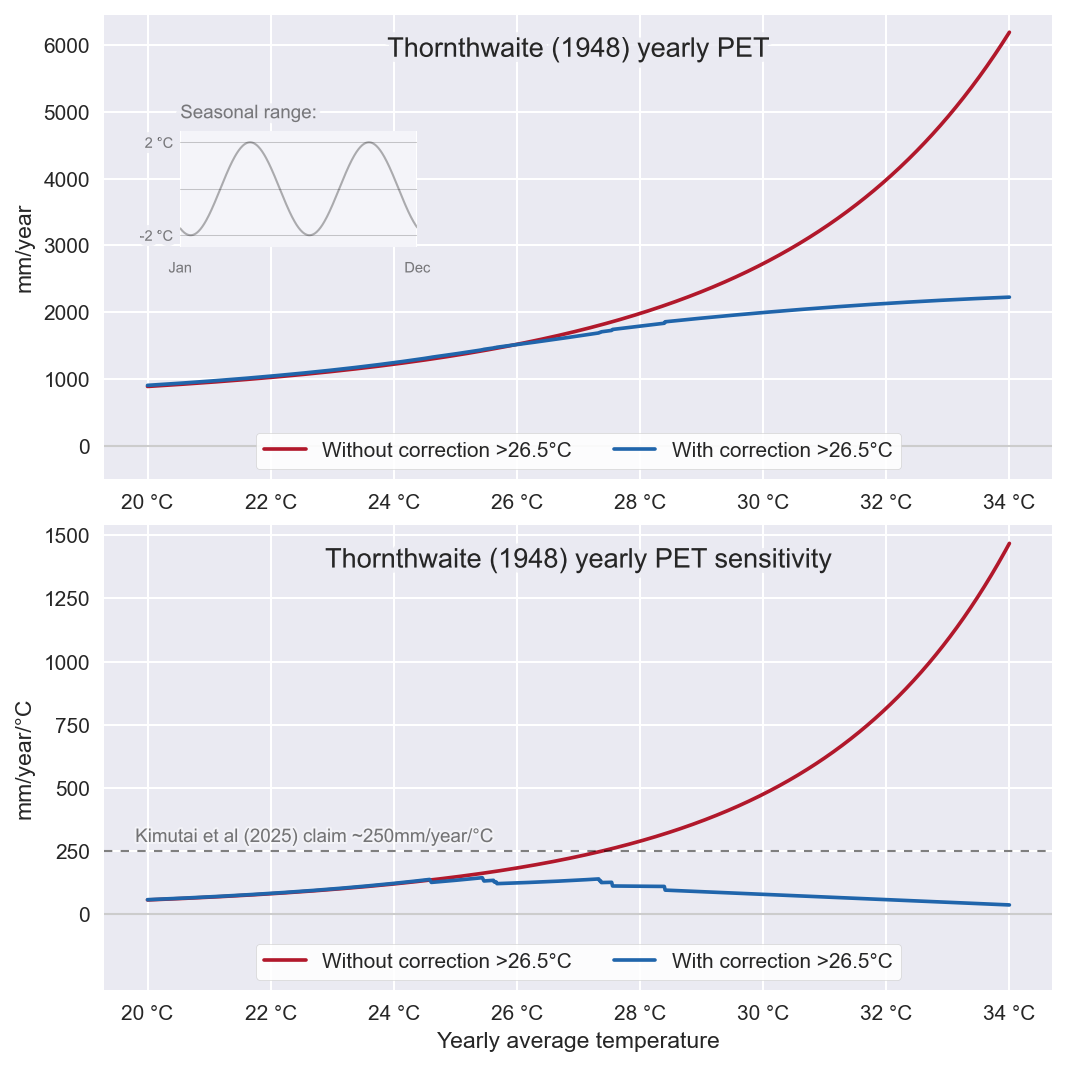
Hun implementatie heeft ook nog een vreemde fout in de coëfficiënt van een van de vergelijkingen. Een fout je vaker in de wetenschappelijke literatuur tegenkomt (welke ze niet citeren), maar niet overeenkomt met Thornthwaite (1948) welke ze citeren. Voor het resultaat is de invloed daarvan beperkt, maar het is wel buitengewoon slordig en niet zoals het hoort in de wetenschap. Je citeert wat je gebruikt, niet meer en niet minder. Het maakt reproductie onnodig ingewikkeld.
Nog een fout in hun implementatie (het houdt niet op...) is hoe ze corrigeren voor de lengte van de maand. De methode beschreven door Thornthwaite geeft in eerste instantie een potentiële verdamping die geldig is voor 30 dagen van elk 12 uur daglicht. Dit wordt dan lineair gecorrigeerd op basis van de werkelijke lengte van de maand en daglicht.
Conceptueel wordt dat:
factor = (n_dagen_in_de_maand / 30) * (gemiddelde_daglengte / 12)
De uiteindelijke hoeveelheid voor een maand is dan "mm_maand = mm_30dagen * factor", redelijk rechttoe-rechtaan.
De correctie voor daglicht gaat goed, maar het KNMI gaat dan de fout in door de "30-dagen hoeveelheid" toe te kennen aan maand, ongeacht hoeveel dagen die maand heeft. Vervolgens rekenen ze dit alsvolgt heen en weer:
mm_dag = mm_30_dagen / n_dagen_in_de_maand
kg_m2_s = mm_dag / 86400
mm_maand = (kg_m2_s * 86400) * (365.25/12)
Effectief betekend dat het KNMI die factor berekend als:
factor = ((365.25/12) / n_dagen_in_de_maand ) * (gemiddelde_daglengte / 12)
Buitengewoon vreemd uiteraard. Die laatste omzetting (365.25/12) is het gevolg van de automatische eenheid conversie die ze gebruiken (Python Pint library). Die zet een maand altijd om naar een periode van 30.4375 dagen, ongeacht de daadwerkelijke lengte van de maand. Mijn beste duiding is dat het KNMI werkelijk geen idee heeft waarmee ze bezig zijn, de software die ze gebruiken niet begrijpt, en ook het resultaat niet controleert.
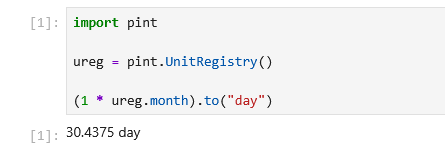
Dat hele conversie-drama bij elkaar geeft per maand de volgende over/onderschatting uitgedrukt in procenten:
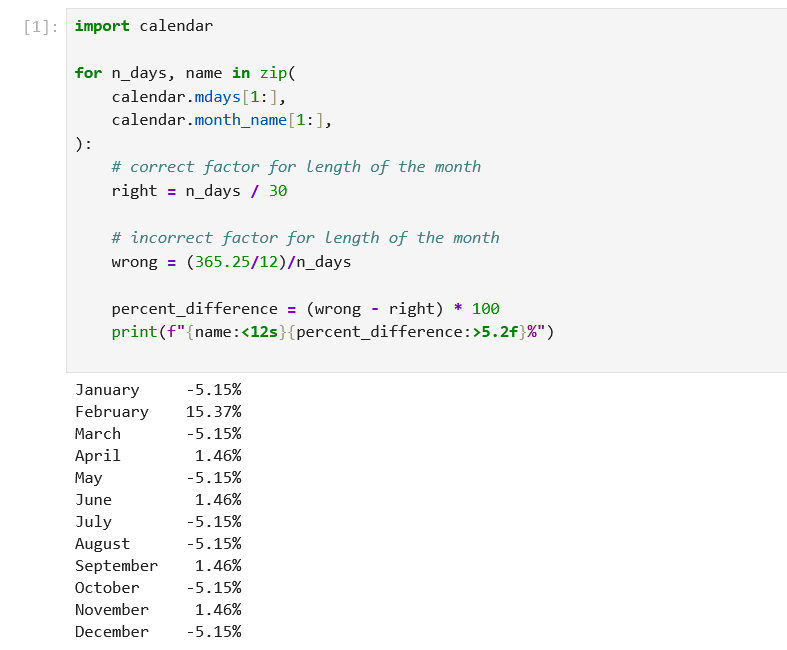
Geluk bij een ongeluk is dat zoals gezegd voor de SPEI-24 de data pas vanaf 1980 beschikbaar is, vanaf dan zijn er enkel positieve temperatuurafwijkingen dus dat probleem speelt wel maar heeft geen effect.
Voor de regressie met temperatuur is het effect dan alsvolgt, hun figuur 6a:
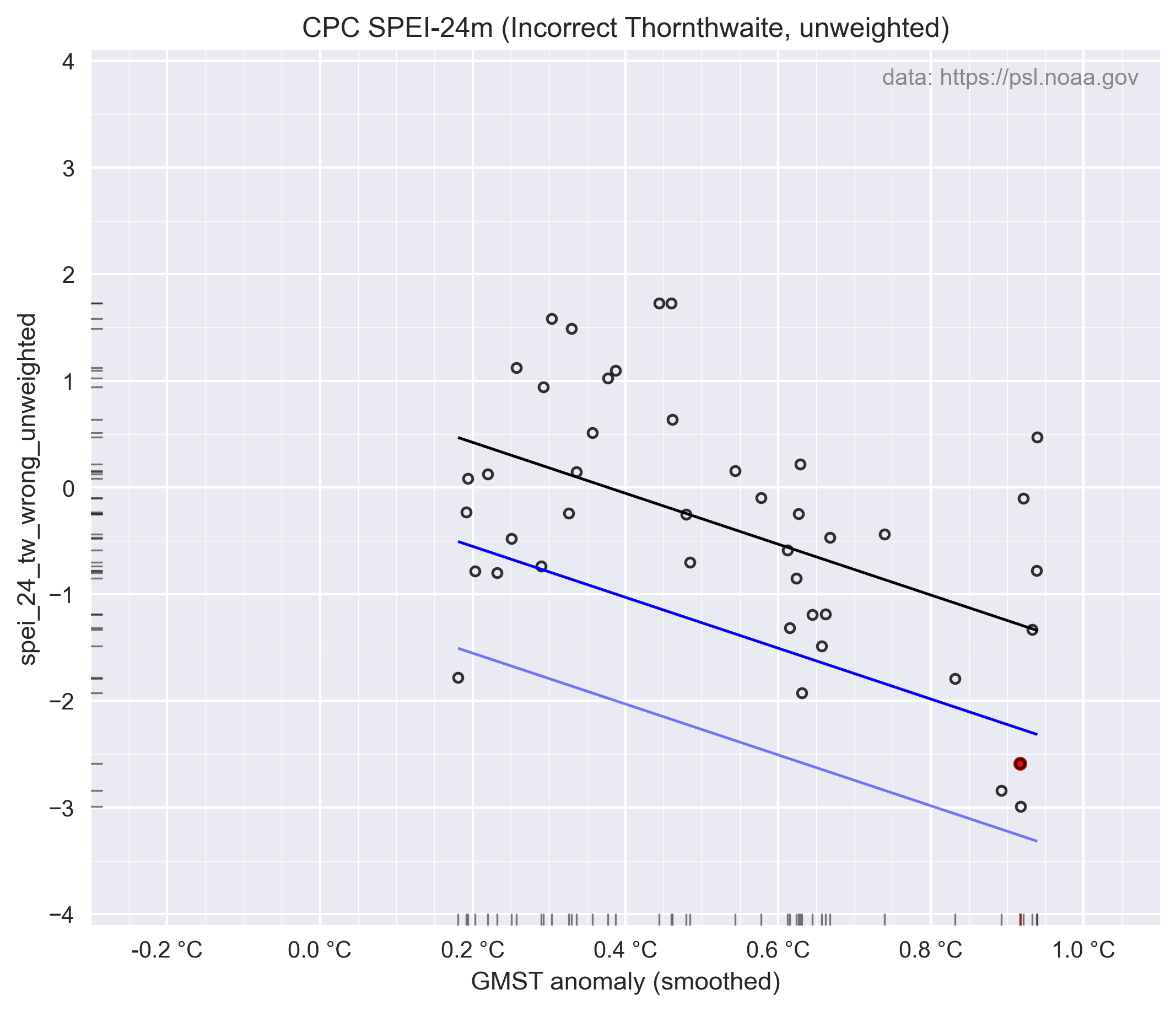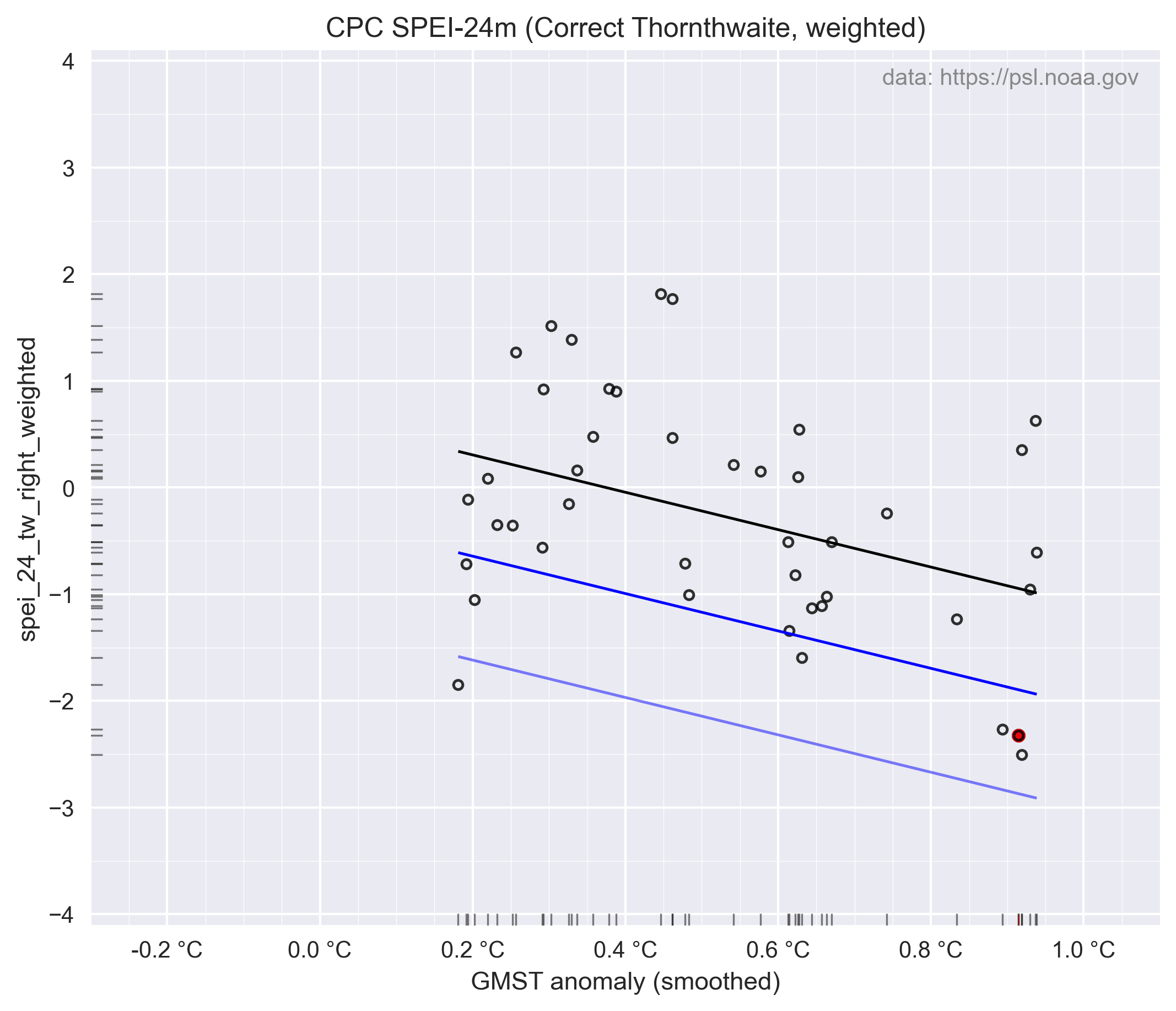
En de bijbehorende "probabilty-ratio", hun figuur 6b. Merk op dat de x-as in log10 is, het verschil is veel groter dan het visueel lijkt.
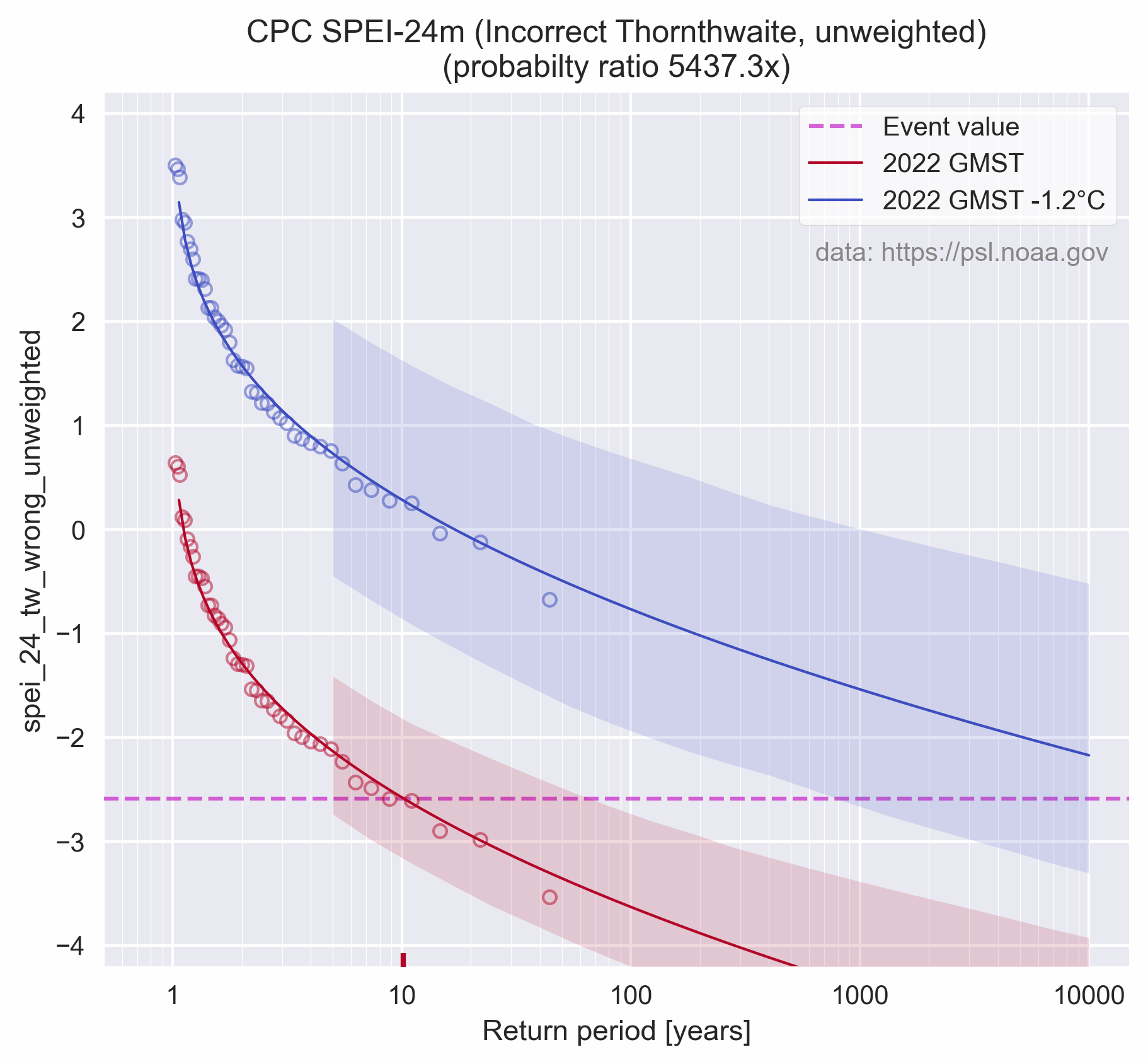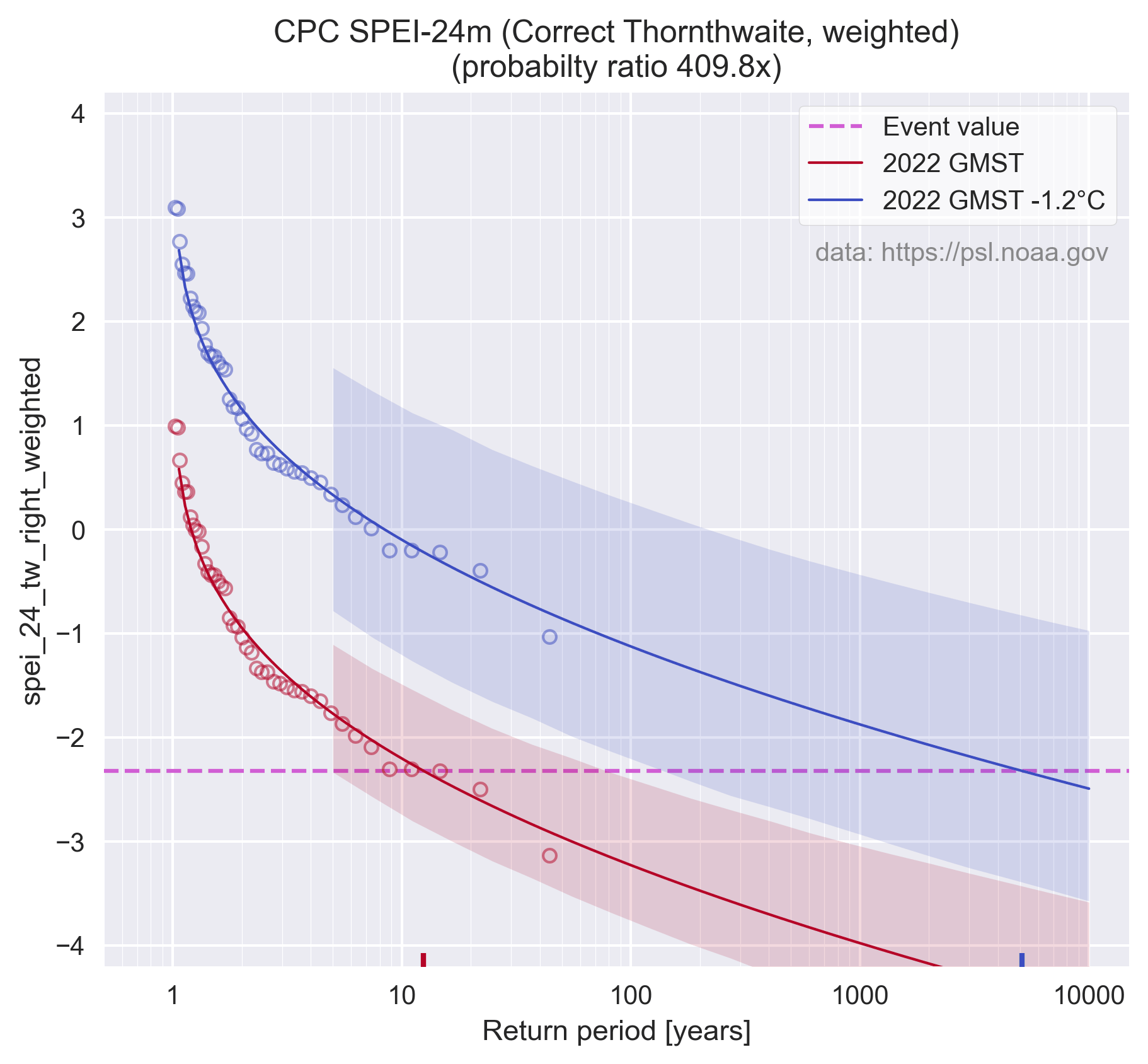
Mijn replicatie is behoorlijk maar niet perfect, de in de studie genoemde probabilty-ratio van 5500x voor de CPC SPEI-24 is bij mij 5437.4x. Na het oplossen van de bovengenoemde implementatiefouten (en nog wat andere) neemt dat af tot 409.8x. Dus het "effect van klimaatverandering" op de onderzochte droogte wordt dus een heel stuk minder. Dat is echter nog steeds met de wat mij betreft volstrekt ongeschikte Thornthwaite (1948) methode.
Persoonlijk vind ik de hele opzet van de studie buitengewoon bedenkelijk. Met name hoe de SPEI-24, wat letterlijk al een maat van waarschijnlijkheid is, wordt opgeblazen door de regressie met de wereldwijde temperatuurafwijking. Omdat in dit geval de neerslagtrend verwaarloosbaar klein is wordt de trend in de SPEI-24 volledig bepaald door de lokale temperatuur, die als gevolg van de implementatiefouten extreem gevoelig is. Effectief doen ze dus een regressie tussen wereldwijde en lokale temperatuur, en uiteraard zit daar een correlatie tussen. Er is wat mij betreft echter geen reden om de maat (SPEI-24) die al een functie is van lokale temperatuur dan nogmaals lineair te corrigeren met de wereldwijde temperatuur. Het wekt op mij de indruk dat het effect van temperatuur twee keer wordt toegepast (lokaal + wereldwijd). De invloed van klimaatverandering uit zich uiteraard (met name) in de lokale temperatuur, de wereldwijde temperatuur is meer een statistische aggregatie achteraf, die niet causaal doorwerkt in lokale effecten. Voor wie het zich afvraagt, de "locatie" van de Normaalverdeling (wat empirisch gezien het gemiddelde van de data is) wordt lineair geschaald met de wereldwijde temperatuur. Ik begrijp ook niet waarom ze niet direct de gebruikte "Generalized Logistic" distributie voor de SPEI-24 schalen, ook daar zit een enorme onzekerheid in die nu niet wordt meegenomen in hun onzekerheidsmarge (via bootstrapping).
Dat gezegd hebbende; als ik een steelman-argument zou moeten geven voor "dit type" onderzoek is de gemakkelijkste verbetering om Thornthwaite (1948) te vervangen voor bijvoorbeeld de "modified-Hargreaves" methode, beschreven door Droogers & Allen (2002). Die methode is nog steeds erg simpel, werkt op maandelijkse stappen (voor een sterk niet-lineair proces) en heeft enkel de maandelijkse minimum/maximum temperatuur en de neerslag nodig, welke binnen deze studie al beschikbaar zijn. Het gebruik van de dagelijkse gang (tmax - tmin) is een flinke verbetering omdat die sterk beïnvloed wordt door verdamping (koeler overdag) en de hoeveelheid vocht in de lucht die dat oplevert (minder afkoeling snachts). De dagelijkse gang verschilt enorm tussen bijvoorbeeld tropen en woestijnen als de Sahara. Zelfs in Nederland zie je bij droogte een sterkere dagelijkse gang (en vergelijkbaar een te hoge Tx in modellen als GFS als die "te droog" zitten).
Persoonlijk zou ik het alsnog niet doen, er is geen enkele reden om aan te nemen dat dergelijke extreem empirische methoden geldig zijn in een "nieuw" klimaat, laat staan dat je tijdens een extreme droogte tot in detail iets kan zeggen over de invloed van klimaatverandering. Dat laatste gaat meer over de gevoeligheid (met temperatuur) wat veel lastiger correct te modelleren is dan enkel de absolute hoeveelheid goed te krijgen. Zo'n methode is geschikt om een grootschalig idee te krijgen van de totalen (van verdamping), de invloed van klimaatverandering op verdamping eruit opmaken is heel iets anders wat mij betreft. Extreem weer zit min of meer per definitie niet goed gevat in dergelijke empirische relaties.
Pas ik die modified-Hargreaves methode toe dan neemt de probabilty-ratio verder af van de eerder genoemde 409.8x met de correctie implementatie van Thorntwaite (1984) tot 1.4x met modified-Hargreaves (Droogers & Allen 2002). De vergelijkbare weergave van figuur 6a & 6b worden dan: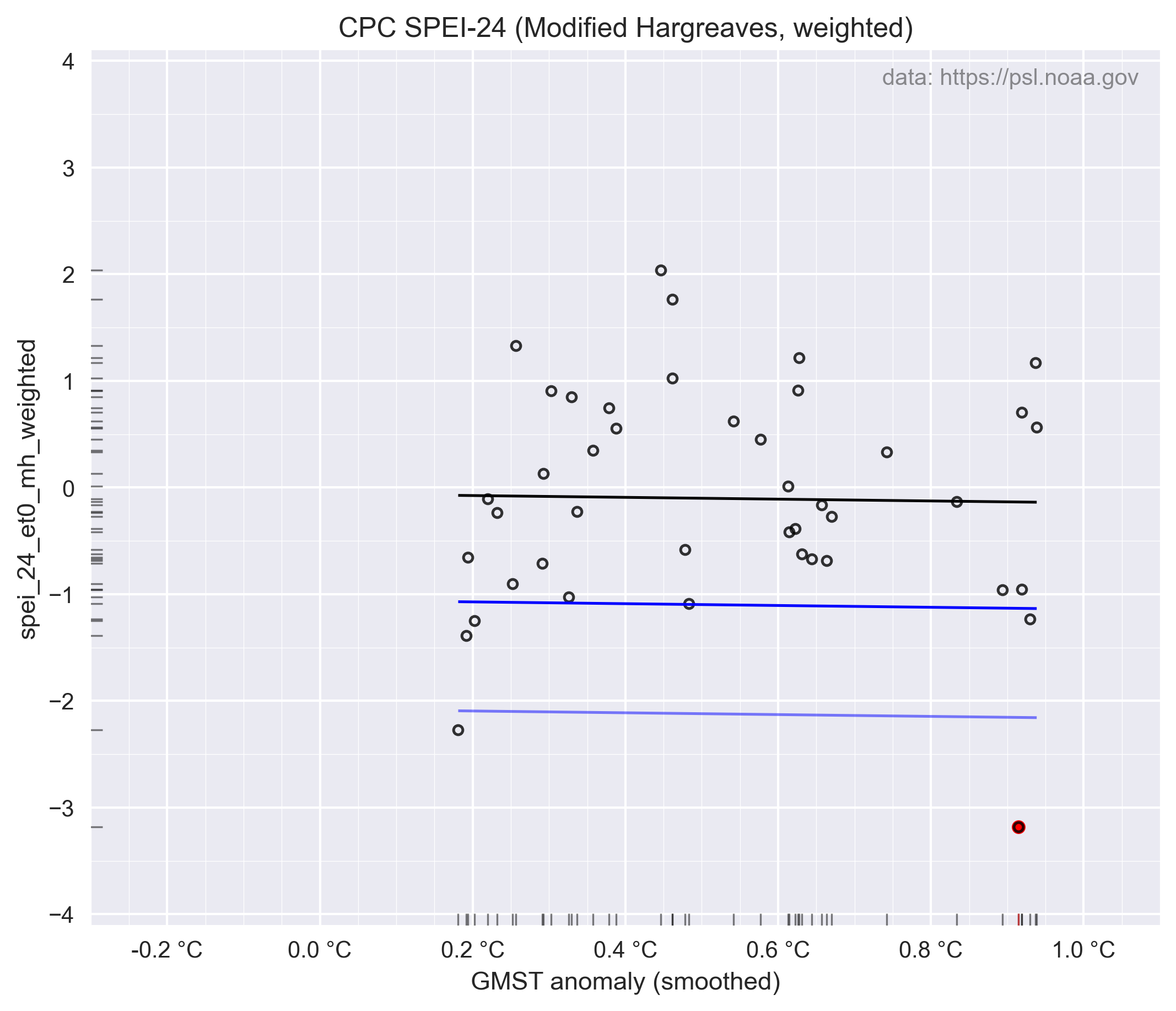
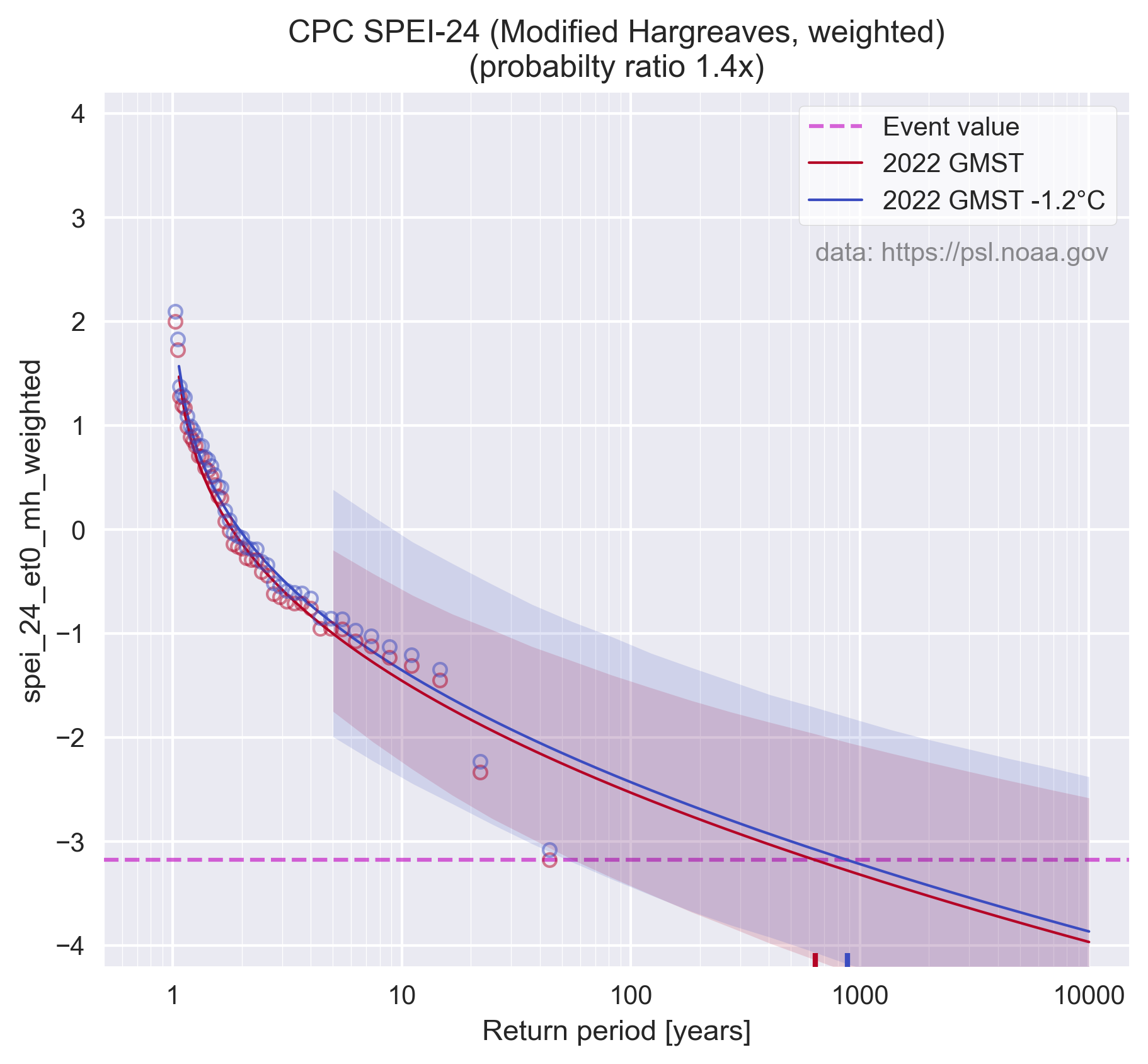
Ironisch genoeg zorgt de drang van het KNMI om deze droogte aan klimaatverandering te koppelen er ook toe dat de droogte zelf (hun "event") minder extreem wordt (een hogere SPEI-24) ten opzichte van bijvoorbeeld modified-Hargreaves. Zie de rood gearceerde stip in de regressie hierboven, die heeft een lagere SPEI-24 waarde dan bij het gebruik van Thornthwaite (en staat meer op zichzelf als een daadwerkelijk extreme gebeurtenis.
Dit komt omdat de onrealistische gevoeligheid van hun foute Thornthwaite implementatie ook in recente niet-droge jaren hoog uitslaat, enkel omdat de temperatuur in de loop van de jaren langzaam oploopt. Relatief lijkt 2021-2022 daardoor minder extreem dan het was. De onrealistische gevoeligheid blijkt ook al uit bijvoorbeeld hun figuur 7. Dit laat ongeveer een toename zien van 600mm voor 24-maanden bij 1.2°C verschil. Dat is dus ongeveer 250mm/jaar/°C, wat overeenkomst met zo'n 2.5x Clausius-Clapeyron. Je zal vast lokale verschillen kunnen vinden in hoe hoog een dergelijke schaling daadwerkelijk is, maar bij 2.5x CC moeten er toch wel wat alarmbellen afgaan en zou je wat mij betreft op z'n minst alles moeten double-checken en met een goede onderbouwing komen waarom dat een juiste uitkomst is. Die is er niet in dit geval, het is volledig een model-artefact als gevolg van de onjuiste implementatie van een onjuist model.
Los van deze gigantische puinzooi is mijn voornaamste les hiervan hoe extreem gevoelig de methode van het KNMI is voor ook maar de kleinste verandering. Dat is vooral het gevolg van het herhaaldelijk toepassen van statistische distributies (Generalized Logistic -> Normal) en het "dubbel tellen" van de temperatuur (lokaal + wereldwijd). Zelfs de datatypen waarin je rekent beginnen duidelijk zichtbaar te worden in de uitkomsten (single vs double), wat het nogal een gedoe maakt om het redelijk te reproduceren. En voor zover dat niet is gelukt zijn er nog wel wat losse eindjes:
- De code in de repo (genoemd in hun eerste rapport; Kimutai et al 2023) komt duidelijk niet overeen met de gepresenteerde resultaten. Wel ongeveer, maar niet exact.
- Er is geen versioning voor wat betreft de vele libraries die gebruikt worden
- De invoerdata (CPC) zit boordevol extreme outliers (bv tmin tot -60°C). Zowel in het rapport als de code zie ik niks terug over bewerken/filteren, opvullen van ontbrekende dagen etc.
- ?
Die punten zijn mij te vaag om er op goed geluk iets mee te doen, de verschillende mogelijkheden waarin een verschil kan zitten zijn te talrijk. Als KNMI meer duidelijkheid geeft over hun methode zal ik een verdere poging wagen.
Het KNMI doet er nog een schepje bovenop in hoe ze de resultaten communiceren, zie bijvoorbeeld de artikelen op nos.nl & knmi.nl die ik hierboven al gaf. De claim dat verdamping toeneemt is volstrekt onzin, en dat raakt exact aan de kritiek die Henk de Bruin ruim tien jaar geleden al uitte. Er viel in de twee jaar waar deze studie over gaat significant minder regen, en in een gebied zonder aanvoer van water (of stuwdammen / fossiele voorraden zoals bv Libië wat betekent dat het onvermijdelijk is dat de verdamping omlaag gaat. Voor verdamping is water nodig, dat is niet ingewikkeld.
wat betekent dat het onvermijdelijk is dat de verdamping omlaag gaat. Voor verdamping is water nodig, dat is niet ingewikkeld.
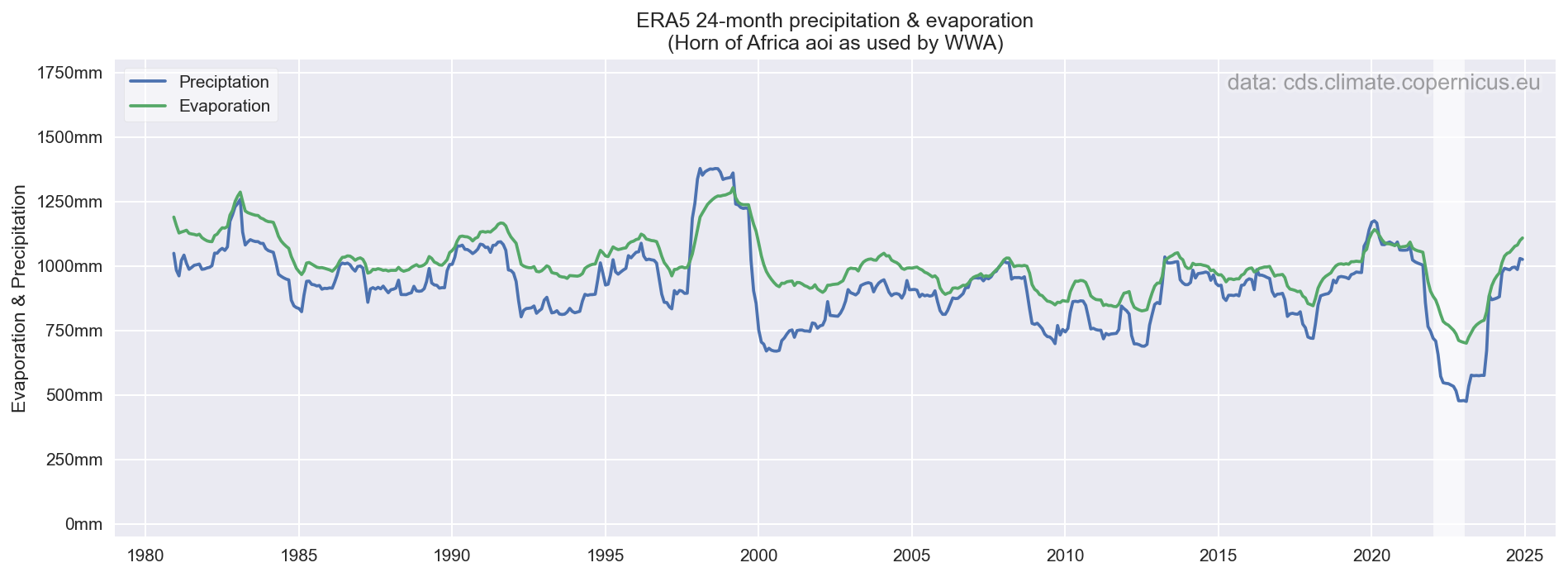
Op basis van ERA5, voor hetzelfde gebied, is dat ook duidelijk te zien. Onderstaande grafiek is op basis van dezelfde 24-maanden als gebruikt in de studie (dus per jaar, niet lopend per maand...). Binnen de periode van deze studie (1980-2022) is meteen duidelijk dat zowel de neerslag als verdamping het laagste is voor 2022, verdamping gaat dus duidelijk omlaag, niet omhoog. Nu is ERA5 wellicht niet de allerbeste bron voor verdamping, maar het zal op dit regionaal niveau de trend (omlaag vs omhoog) wel te pakken hebben. Andere datasets (GLEAM, Wapor etc) zullen een vergelijkbaar signaal geven, maar ongetwijfeld met een iets andere absolute hoeveelheid.
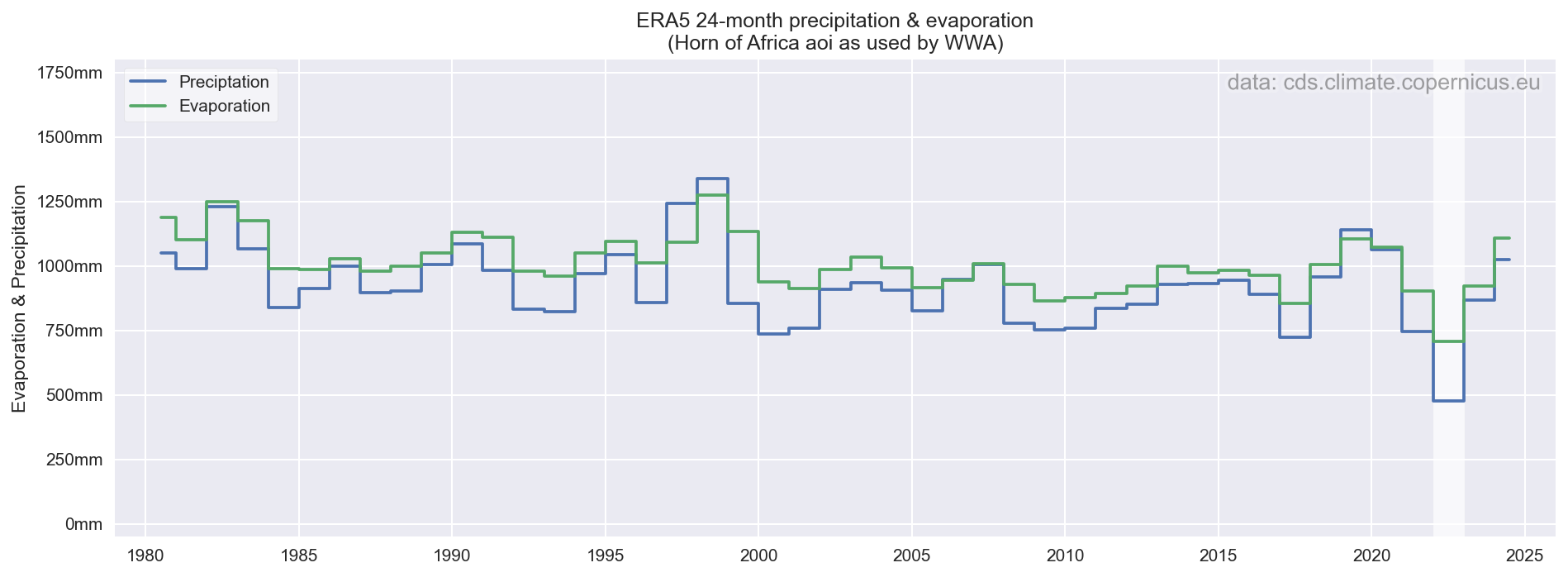
Een weergave van dezelfde data maar dan als lopende 24-maandelijkse som is wellicht iets intuïtiever. Dat laat ook zien dat de droogte van 2021-2022 zoals gedefinieerd in deze studie perfect overeenkomt met eind 2022, waardoor de aggregatie op jaarbasis weinig invloed heeft op de gebruikte waarde. Voor eerdere droogtes (bv 2009, 2012/2013 is die "uitlijning" met het kalenderjaar minder gelukkig en wordt de waarde significant hoger door die aggregatie naar kalenderjaren.
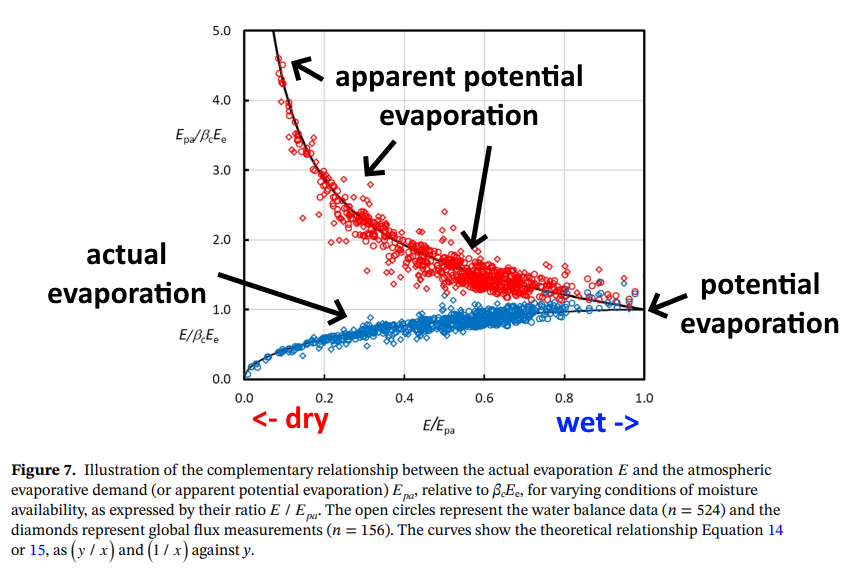
De reden dat KNMI beweerd dat het omhoog gaat is omdat ze (ogenschijnlijke) potentiële verdamping modelleren, waarvan het minstens al sinds Bouchet (1963) duidelijk dat die in tegengestelde richting ontwikkelt tijdens een toenemende droogte. Verdamping gaat omlaag (er is geen water), mede daardoor neemt de luchttemperatuur toe en relatieve luchtvochtigheid af, en dus gaat de (hypothetische) potentiële verdamping omhoog. Beide zijn een keerzijde van exact dezelfde medaille, onlosmakelijk met elkaar verbonden:
Edit;
In de eerste versie stond een voorbeeldje voor de fout met de correctie van de maand. Dit liet enkel de foute correctiefactor zien in de studie gebruikt wordt. Omdat de goede correctiefactor het resultaat ook veranderd en in dit geval in de tegenovergestelde richting werkt is het uiteindelijk verschil nog groter voor de maanden zonder 30 dagen.
De afbeelding in de bovenstaande post is inmiddels aangepast en komt nu overeen met de tekst.